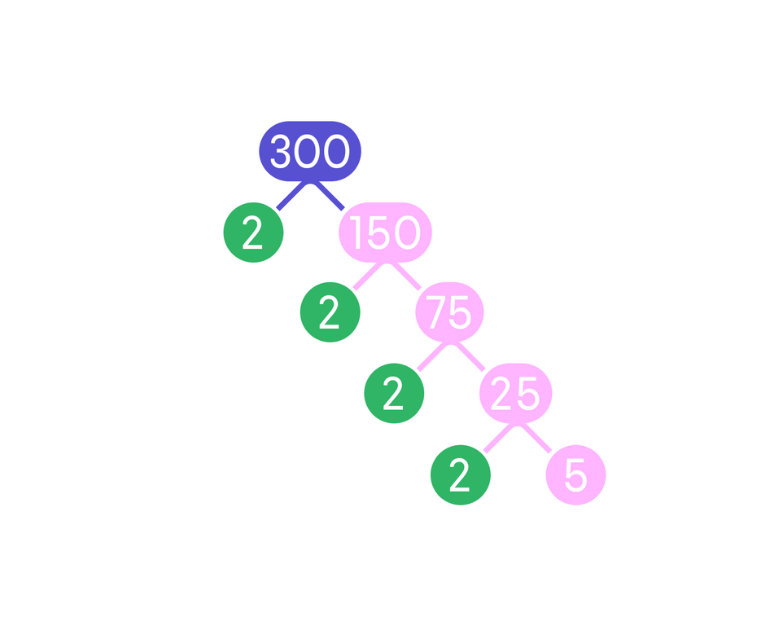
Express 300 as a product of its prime factors

Prime factorisation can be a challenging topic for students of all ages, especially when dealing with numbers like 300, which involve factors like 2, 3, 5, and 10. 

It can be difficult to know where to begin when trying to break down a number like 300, which is a product of two 2s, a 3, and a 10. This is particularly relevant for students who are studying numbers divisible by 6 and 30, as 300 is 50 times 6 and 10 times 30.

Whether you're studying for an exam or just looking to improve your Maths skills, this guide will provide you with an efficient and educational tool for mastering prime factorisation. Plus, we will introduce a free online tool later in this guide that can further simplify the process of prime factorisation for you. 

What Is Prime Factorisation?

First, let's define what we mean by prime factors. Prime factors are the prime numbers that can be multiplied together to get a given number. 

For example, the prime factors of 12 are 2, 2, and 3, since 2 x 2 x 3 = 12. Now, let's apply this concept to the number 300.

Steps:

• Divide 300 by the smallest prime factor possible, which is 2. This gives us 150.
• Divide 150 by 2, which gives us 75.
• Divide 75 by 3, which gives us 25.
• Divide 25 by 5, which gives us 5.
• Divide 5 by itself, which gives us 1.

Now that we have broken down 300 into its prime factors, we can write it as:

300 = 2 x 2 x 3 x 5 x 5

This is the prime factorisation of 300.

An Educational Tool For Prime Factor Mastery

At times, it's quite challenging to keep up with the pace of your classroom teacher. With the rise of the internet, educational tools are readily available to help students of all ages understand complex topics enjoyably and interactively. 

One of these educational tools is the "Prime Factorisation Calculator," which is available for free online. This tool can help you achieve a deeper understanding of prime factors quickly and efficiently during your study time.

How does it work? All you have to do is input any number, and the calculator will instantly display the prime factorisation of the given number.

Conclusion

Prime factorisation is a useful tool for many areas of Maths, including fractions, geometry, and algebra. By mastering this concept, students can greatly improve their understanding and success in these subjects. Breaking down 300 into its prime factors is just one example of how prime factorisation can be applied in the real world. With practice and study, students can become experts in prime factorisation and use it to solve even more complex Maths problems. Understanding the role of factors like two (2) in prime factorisation can be a significant step in this learning process.

So don't be afraid to dive in and start practising – prime factorisation may just become your new favourite Maths concept!