How do I find the intersection of a line and a curve?

When it comes to the world of Maths, few topics are as important as the intersection of a line and a curve. Understanding how to navigate these intersections is an essential skill for students looking to succeed in a wide range of mathematical disciplines, from Data Science and Engineering to Actuarial Sciences and beyond.

This blog covers how to find where a line and a curve intersect. It includes the main equations and concepts you'll need to help you solve this math problem.

Solving for Intersection: Line and Curve Equation Equivalence

The first step in finding the intersection between a line and a curve is understanding the mathematical representations of these shapes. A line can be expressed in the form y = mx + b, where m is the slope of the line and b is the y-intercept (where the line crosses the y-axis).

Conversely, a curve is often represented by a more complex formula, typically involving higher-order polynomials or trigonometric functions.

To determine the intersection point, it's necessary to set the line's expression and the curve's formula equal to each other and solve for x and y. 

• For instance, consider a line described by y = 2x + 1 and a curve represented by y = x^2 - 2. To find their intersection, align their formulas 2x + 1 = x^2 - 2

• From here, we can rearrange the expression into a standard quadratic form: x^2 - 2x - 3 = 0

• Using the quadratic formula, we can solve for the two possible values of x, and we get: x = 3 or x = -1

Plugging these values back into the equation for the line or curve will give us the corresponding values of y at each intersection point.

Intersection Insights: Equating Equations for Line and Curve

While solving for line and curve intersections might seem straightforward on paper, visualising and understanding their geometrical significance can be challenging. A helpful strategy for gaining insight is to graph both the line and the curve, allowing you to identify where they intersect visually.

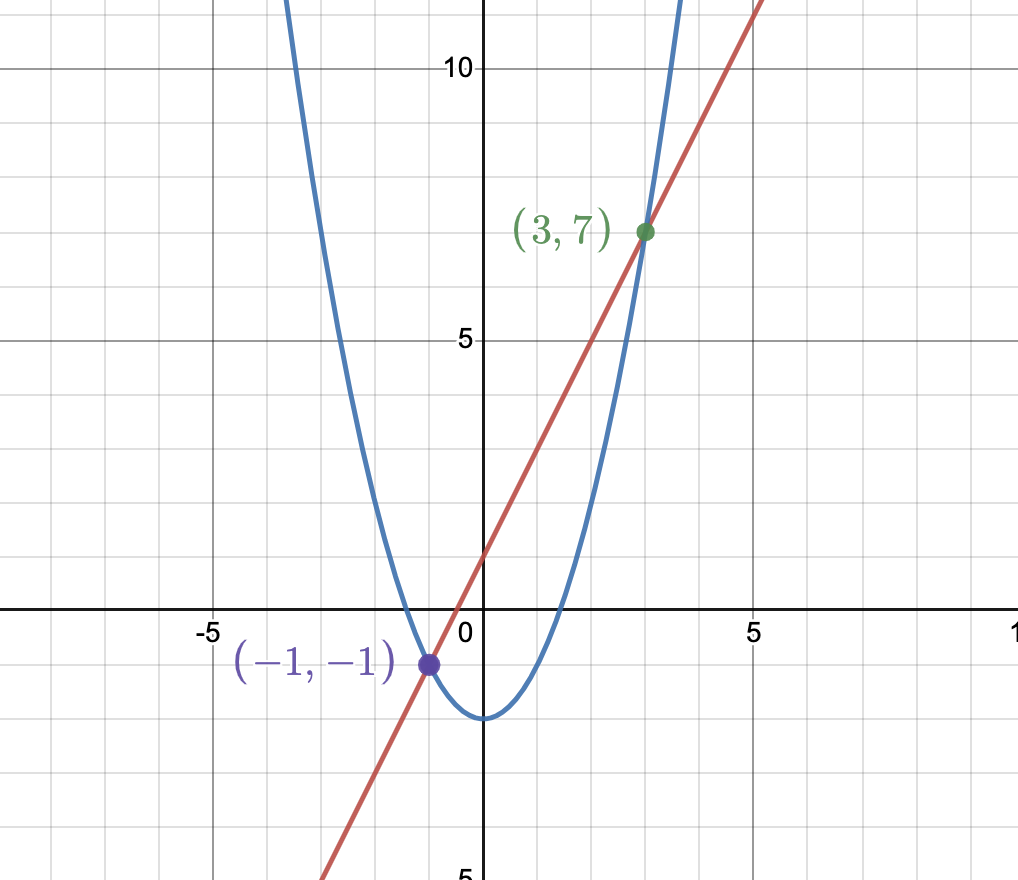
For example, consider the line y = 2x + 1 and the curve y = x^2 - 2. We can plot these equations on a graph and see that they intersect at two points: (3,7) and (-1,-14). By looking at the graph of the equations, we can get a better sense of the underlying geometry and intuition behind the intersection points.

Conclusion

If you want to pursue a career in Maths, as a student, it's essential to understand how lines and curves intersect. By mastering the fundamental equations, concepts, and techniques involved in finding these intersections, you, as a student, can better understand how mathematical shapes behave. This understanding is vital for your professional growth and a crucial part of your Maths revision process.

Whether you're working in engineering, physics, data analysis, or any other field that relies on mathematical models, finding line-curve intersections is a must-have skill that will help you excel in your chosen profession. Engaging deeply with this topic is beneficial for practical application and enhances your revision study.