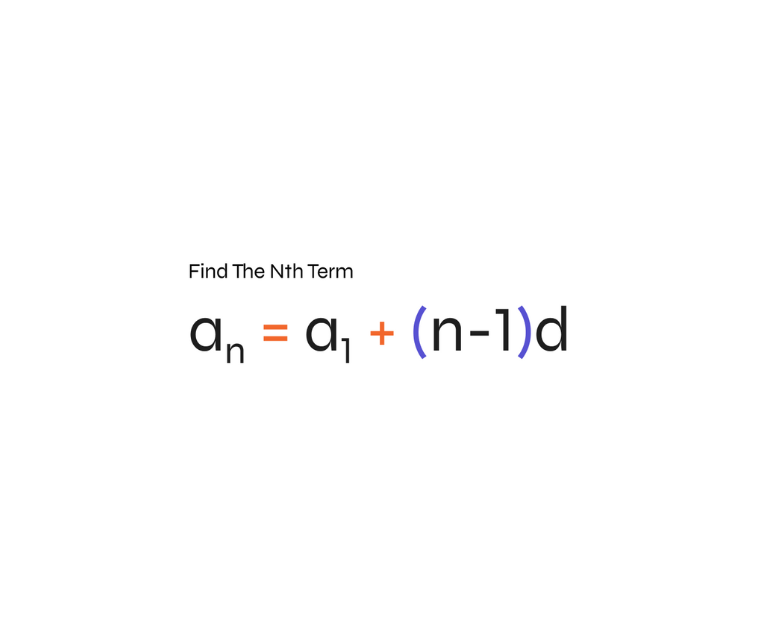
How Do You Find the nth Term? A Comprehensive Guide

Finding the nth term of a sequence is a fundamental skill in mathematics, essential for solving problems in algebra, calculus, and beyond. Whether you're tackling homework, preparing for exams, or diving into advanced math, understanding how to find the nth term can simplify complex problems and reveal hidden patterns. In this post, we’ll break down the process step by step, explore different types of sequences, and provide real-world examples to illustrate the concepts.

What Is the nth Term?

The "nth term" of a sequence is a formula that lets you calculate any term in the sequence without listing all the previous ones. In other words, if you have a sequence like 3, 5, 7, 9, … you can find the 50th term directly using a formula. The value "n" represents the position of the term in the sequence.

Types of Sequences and Their nth Term Formulas

Different types of sequences use different formulas to determine the nth term. Let’s explore the most common ones.

1. Arithmetic Sequences

An arithmetic sequence is one in which the difference between consecutive terms is constant. This constant is known as the common difference (d).

General Formula:

$Arithmetic Sequences formula$

is the nth term.
$a_{1}$ is the first term.
is the common difference.
is the term number.

Example:
Consider the sequence: 4, 7, 10, 13, …

The first term, $a_{1}$ , is 4.
The common difference, $d$ , is .

Plug these into the formula:

$Arithmetic Sequences formula image 2$

So, the 10th term is:

$Arithmetic Sequences formula image 3$

2. Geometric Sequences

A geometric sequence multiplies each term by a constant ratio to get the next term. This constant is called the common ratio (r).

General Formula:

$Geometric Sequences general formula$

$a_{n}$ is the nth term.
$a_{1}$ is the first term.
is the common ratio.
is the term number.

Example:
Consider the sequence: 2, 6, 18, 54, …

The first term, $a_{1}$ , is 2.
The common ratio, , is 6/2=3.

Using the formula:

$Geometric Sequences how to use$

Thus, the 5th term is:

$Geometric Sequences final formula$

3. Other Sequences

While arithmetic and geometric sequences are the most common, some sequences follow quadratic, cubic, or even more complex patterns. For example, a quadratic sequence might have a general form like:

$other sequence formula$

Finding the coefficients $a$ , $b$ , and $c$ usually involves solving a system of equations based on the first few terms of the sequence.

Step-by-Step Guide: How to Find the nth Term

No matter what type of sequence you’re dealing with, the following steps will help you determine the nth term:

Identify the First Term:
Determine the first term ( $a_{1}$ ) of the sequence. This is your starting point.
Determine the Pattern:
- For Arithmetic Sequences: Calculate the common difference ( $d$ ) by subtracting any term from the subsequent term.
- For Geometric Sequences: Calculate the common ratio ( $r$ ) by dividing any term by the previous term.
Choose the Appropriate Formula:
Use the arithmetic or geometric nth term formula based on the type of sequence.
Substitute and Simplify:
Plug your values into the formula and simplify to get your nth term formula.
Apply the Formula:
Once you have your formula, substitute the value of to find any term in the sequence.

Practical Examples

Example 1: Arithmetic Sequence

Problem:
Find the 12th term of the sequence: 5, 8, 11, 14, …

Solution:

First term $a_{1} = 5$
Common difference

Use the arithmetic formula:

$arithmetic formula step 1$

For $n = 12$ :

$arithmetic formula step 2$

Example 2: Geometric Sequence

Problem:
Find the 6th term of the sequence: 3, 6, 12, 24, …

Solution:

First term $a_{1} = 3$
Common ratio

Use the geometric formula:

$geometric formula step 1$

For $n = 6$ :

$geometric formula step 2$

Why Finding the nth Term Matters

Understanding how to find the nth term is not just a classroom exercise. It has real-world applications such as:

Predicting Future Values: In finance, determining the future value of an investment can sometimes be modelled using arithmetic or geometric sequences.
Pattern Recognition: In computer science, recognizing patterns is crucial for algorithms and data structures.
Engineering Applications: Engineers often use sequences to model loads, stresses, or other regularly changing variables.

By mastering this technique, you can solve a wide range of problems more efficiently.

Tips for Success

Practice Regularly: The more you practice finding the nth term, the more intuitive it becomes.
Double-Check Your Calculations: Small errors in identifying a1, , or can lead to incorrect results.
Understand the Underlying Concepts: Rather than memorizing formulas, focus on understanding why they work. This deep comprehension will help you adapt to various types of sequences.

Conclusion

Finding the nth term of a sequence is a powerful tool in mathematics that opens up a world of problem-solving strategies. Whether you’re working with an arithmetic sequence by adding a common difference or a geometric sequence by multiplying by a common ratio, the process is systematic and logical. By following the step-by-step guide outlined in this post, you can quickly determine any term in a sequence and apply these skills to both academic and real-world problems.

Ready to put your new skills to the test? Start by identifying sequences around you and practice calculating their nth terms. Happy calculating!

Year Group

Subject

Resource

Courses