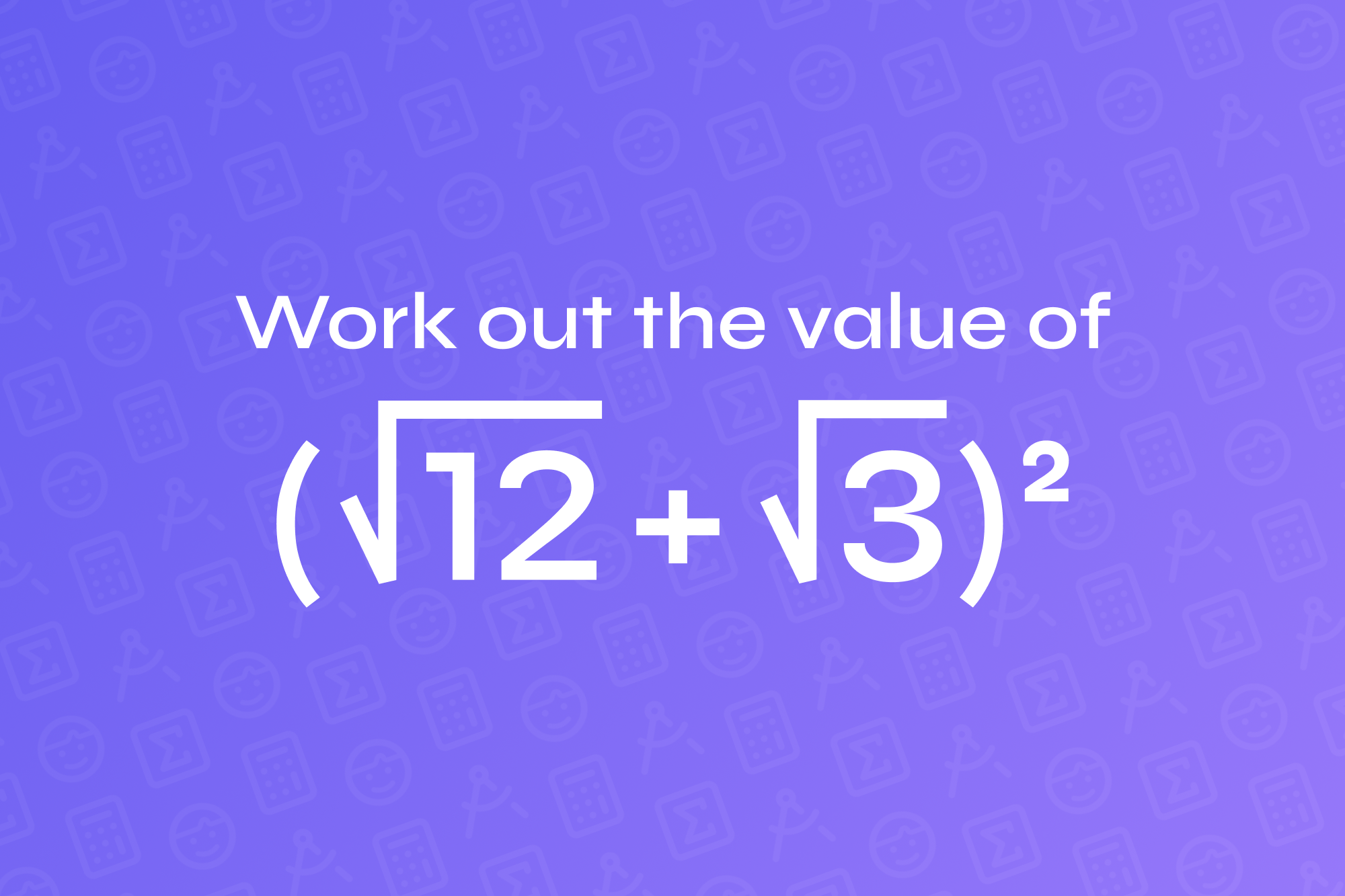
How to find the value of (√12 + √3)² (step-by-step)
When faced with expressions involving radicals, such as (√12 + √3)², it can seem tricky at first glance. However, by applying basic algebraic identities and simplification techniques, you can tackle these problems step by step. This guide will show you how to break down the expression using algebraic rules to find the exact value.
Understanding the square of a sum
The expression (√12 + √3)² represents the square of a sum. To solve this, we use the algebraic identity for squaring binomials:
(a + b) 2 = a2+ 2ab + b2
In this case, 12 is a, and 3 is b.
Applying the algebraic identity
Now, applying the identity to (√12 + √3)²:
(√12 + √3)² = (√12 )² + 2(√12 )(√3) + ( √3)²
This expands the expression into three terms that need further simplification.
Simplification of radical terms
Let’s simplify each part of the expanded expression:
-
(√12 )² = √12 x √12 = 12
-
2(√12 )(√3) = 212 x 3 = 236 = 2 x 6 = 12
-
( √3)² = √3 x √3 = 3
Now, the expanded and simplified terms are:
12+12+3
Final computation and simplification
Finally, summing the simplified terms:
12 + 12 + 3 = 27
Thus, the value of (√12 + √3)² is 27.
Following these steps, you can quickly solve expressions involving radicals using algebraic identities and simplification techniques. This method ensures clarity and accuracy, allowing you to handle similar problems easily.