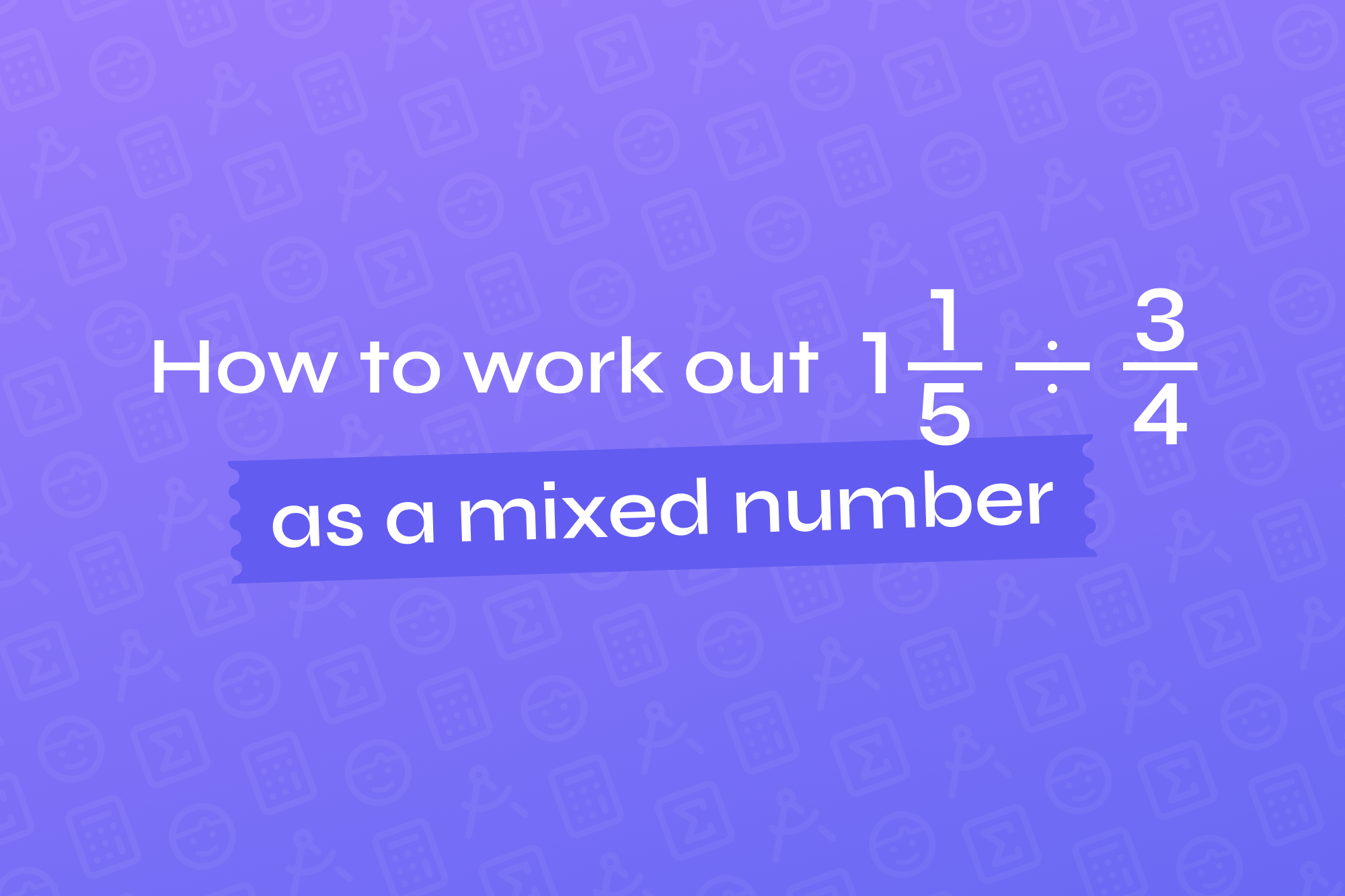
How to work out 1 1/5 divided by 3/4 as a mixed number

Dividing fractions can be tricky, especially when mixed numbers are involved. In this article, we'll learn how to divide 1 1/5 ​ by 3/4​. Understanding how to convert mixed numbers into improper fractions makes division more straightforward.

Importance of converting 1 1/5 to an improper fraction for easier division

Before performing the division, it’s essential to convert the mixed number 1 1/5 ​ into an improper fraction. This step allows us to handle the division more effectively and avoid any complications.

Conversion of the mixed number:

1 1/5 = {(1 x 5) + 1}/5 = 6/5 

Steps to divide the improper fraction by  3/4​

We can proceed with the division once we have converted the mixed number. The rule for dividing fractions states that you should invert the second fraction (the divisor) and multiply.

1. Write the problem with the improper fraction:
   6/5 ​÷ 3/4

2. Invert the divisor:
   6/5 ​x 4/3

3. Multiply the fractions:
   (6 x 4)/(5 x 3) ​ = 24/15

Methods to simplify the resulting fraction to its simplest form

Now, let's simplify 24/15​. To do this, we can find the greatest common divisor (GCD) of the numerator and denominator.

1. Find the GCD of 24 and 15:

• The GCD is 3.

2. Divide both the numerator and denominator by the GCD:
   (24÷3)/(15÷3) = 8/5

3. Convert back to a mixed number if desired:
   8/5 = 1 and 3/5

To learn more about the greatest common divisor (GCD), check out: What is the difference between LCM and HCF. 

Conclusion

In summary, to solve 1 1/5 ÷ 3/4 ​, we first converted the mixed number to an improper fraction, inverted the divisor, and multiplied. The final simplified result is 1 and 3/5​. Mastering these steps will enhance your ability to work with fractions efficiently.

You may also be interested in:

• What is 2/3 + 1/4?

• Express 300 as a product of its prime factors

• How do you calculate a number to the power of a fraction?