Trigonometry tips: When to use sin, cos, or tan – and why
Trigonometry can be challenging at first, especially when deciding whether to use sine, cosine, or tangent in a given problem. In this guide, we’ll break down these trigonometric ratios, explain their applications, and give you tips on how to choose the right one every time.
Fundamentals of trigonometric ratios
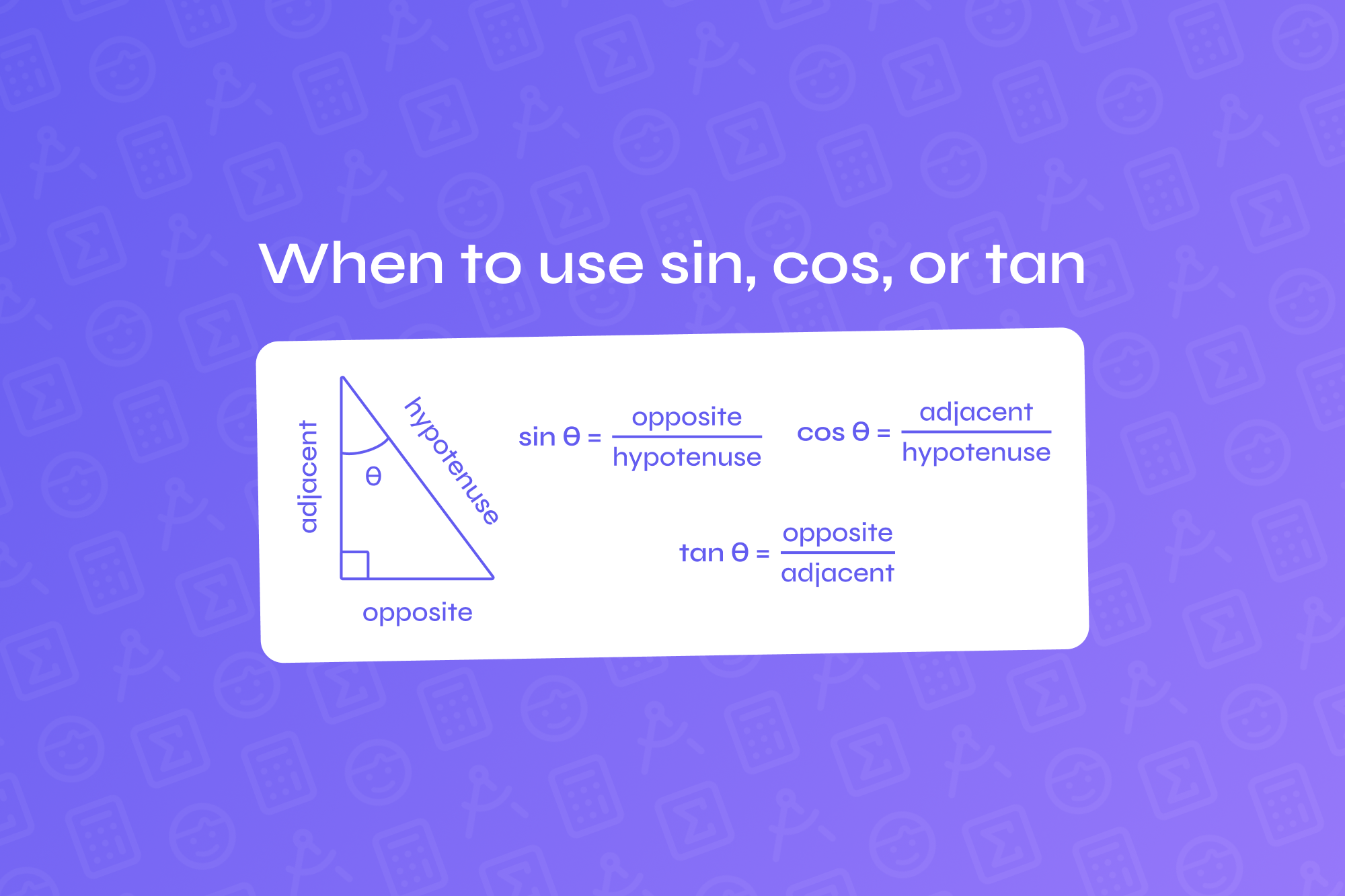
In a right-angled triangle, the three primary trigonometric ratios—sine (sin), cosine (cos), and tangent (tan)—are used to relate the angles to the sides of the triangle.
Here’s a quick breakdown:
-
Sine (sin): Relates the angle to the ratio of the opposite side over the hypotenuse.
-
Cosine (cos): Relates the angle to the ratio of the adjacent side over the hypotenuse.
-
Tangent (tan): Relates the angle to the ratio of the opposite side over the adjacent side.
Remember: the hypotenuse is always the longest side of the right-angled triangle, and the opposite and adjacent sides depend on the angle you're working with.
How to remember the formulas: SOH CAH TOA
A simple and popular way to remember these formulas is through the mnemonic SOH CAH TOA:
-
SOH: Sine = Opposite / Hypotenuse
-
CAH: Cosine = Adjacent / Hypotenuse
-
TOA: Tangent = Opposite / Adjacent
This memory trick can help you quickly recall which trigonometric ratio to use based on the sides of the triangle you are working with.
Practical applications and illustrations
So, when do you use sin, cos, or tan? Let’s look at some situations:
-
Use sin(θ) when you know the hypotenuse and need to find the opposite side, or vice versa.
Example: Given a right triangle where the hypotenuse is 10 cm and the angle θ = 30∘, you can find the length of the opposite side by applying:
-
Use cos(θ) when you need to find the adjacent side or the hypotenuse.
Example: If the hypotenuse is 13 cm and the angle is 60∘, you can calculate the adjacent side by:
-
Use tan(θ) when you only have the opposite and adjacent sides and need to relate them.
Example: If the opposite side is 7 cm and the adjacent side is 3 cm, find the angle θ using:
Conclusion
Understanding when to use sin, cos, and tan is crucial for mastering trigonometry. With practice, these ratios become second nature, and with the help of online tools and tutors, you can sharpen your skills and gain confidence in applying them. Keep practising, and soon, trigonometry won’t seem so intimidating!