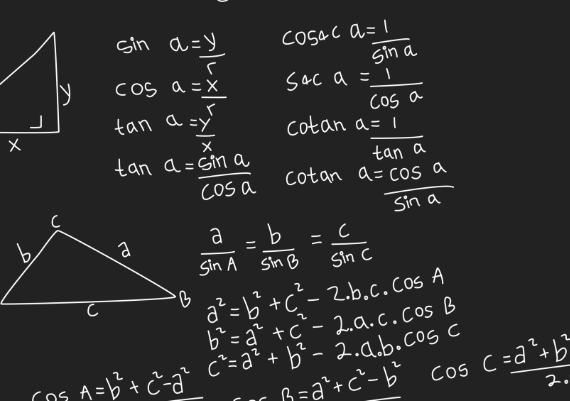
When do I use a cosine rule over a sine rule?

Introduction

As a Maths student, you will often encounter the need to study and apply the sine and cosine rules. These are crucial for navigating trigonometry problems, especially when dealing with unknown sides and angles in triangles. But when should you use a cosine rule over a sine rule? 

This blog post aims to clarify these rules and provide practical insights to aid your study and revision. We’ll equip you with the knowledge to help you make informed decisions when choosing which rule to use, all accessible for free.

The Sine Vs Cosine Rule

The sine and cosine rules serve distinct purposes and are crucial in the study of trigonometry. The sine rule is typically used when working with two sides and an included angle, or when finding an unknown side. To effectively use the sine rule, rearrange it to solve for the missing side length:

sin A/a = sin B/b = sin C/c.

Conversely, the cosine rule becomes relevant with two sides and a non-included angle or when calculating an unknown side. For this, the rule needs to be adjusted:

a² = b² + c² − 2bc cos A.

The choice between these depends on the problem's focus. The sine rule is often more suitable if it involves finding an unknown length. However, for unknown angles, the cosine is preferred.

Another aspect to consider is the problem's complexity. If both equations could apply, opting for the simpler and faster one is advisable - often, the sine equation.

Real-world Applications

Both cosine and sine are fundamental trigonometric functions that play indispensable roles in numerous fields of study, ranging from mathematics and physics to engineering and architecture. These functions are versatile tools with practical applications that extend far beyond their theoretical foundations.

The cosine function, for instance, is precious in vector analysis. In this field, it serves as a crucial tool for determining a vector's magnitude and direction based on its components. Engineers and physicists often leverage the cosine function to analyse forces and motions, making it a cornerstone in various scientific disciplines.

On the other hand, sine, another essential trigonometric function, finds practical applications in calculating the area of non-right-angled triangles. This application is especially significant in fields like geometry and surveying, where accurate measurements and calculations are essential. The sine function's ability to provide insights into triangular geometry contributes to design, construction, and land surveying advancements.

• Additional Applications of Sine and Cosine Functions:
• Electrical Engineering: Modelling AC waveforms in circuits.
• Sound Wave Analysis: Describing and analysing audio signals.
• Astronomy: Calculating celestial body positions.
• Navigation and GPS: Determining latitude, longitude, and course angles.
• Computer Graphics: Creating animations and game graphics.
• Physics: Describing wave mechanics in quantum and optical physics.
• Architecture: Designing structures with angular properties and curves.

Related: Trigonometry and its Applications in Real Life

Conclusion

In conclusion, the choice hinges on the nature of the trigonometry problem. The sine method is typically used to find a missing length or when two lengths and an included angle are known, whereas the cosine method is used for unknown angles or with two lengths and a non-included angle.

Evaluating the problem's complexity and specific requirements is vital to deciding which equation to apply. Understanding their differences will enhance students' ability to tackle trigonometry problems quickly and confidently. Remember, these resources are free and available to help you excel in Maths. Good luck with your Maths revision!