Ideal Gas
Brook Edgar
Teacher

Contents
Explainer Video
Introduction to Ideal Gas Laws
Ideal Gas
Ideal gases follow the three gas laws, Boyle's law, Charles's law, and the Pressure law and have the following properties:
The molecules have a negligible size/volume compared to the volume of the container.
All collisions are elastic.
The time of a collision is negligible compared to the time between collisions.
Gas molecules exert no forces on each other except during impact (no potential energy).
The motion of the gas molecules is random, and the molecules are all identical/have the same mass.
Remember: AQA often asks you to state at least three gas laws in exams. Learn the first three off by heart!
Boyle's Law
For a constant mass of gas at a constant temperature, the pressure exerted by the gas is inversely proportional to the volume it occupies.

The use of the microscopic behaviour of the particles to explain their macroscopic properties is known as the kinetic theory of gases.
Reminder: In physics we often use to represent an unknown constant.
If the volume decreases, the particles have less distance to travel before hitting the walls of their container. However, as the particles keep moving at the same speed (as the temperature is constant), from the equation, , the time between collisions with the walls of the container must decrease. This means there are more frequent collisions with the walls of the container.
*****image
*********
As the time between collisions with the walls of the container decreases, the force per unit area increases, for the same change in momentum; thus, the pressure also increases.
Remember: Boyle sounds like boiling, which suggests an increase in temperature – but since it's spelt differently, it has nothing to do with temperature. Instead, it relates pressure and volume (my key tip to help you remember the gas laws).
Charles's Law
For a constant mass of gas at a constant pressure, the volume occupied by the gas is directly proportional to its absolute temperature.
(a constant)
Note: Temperature must be in Kelvin.

As the temperature increases, the mean kinetic energy and thus the mean speed of the particles both increase. This leads to a greater change in momentum when the particles collide with the walls of the container, resulting in an increased force per unit area, . But as the pressure must remain constant, the time between collisions must increase. Therefore, the particles must travel a greater distance before colliding with the walls of the container, which means the volume increases.
******image *******
Remember: You must say mean kinetic energy, as not all particles move faster when the temperature increases – but the mean speed of the particles does increase. Some particles will move slower or faster than this mean speed because the motion of particles is random.
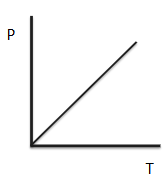
Pressure Law
For a constant mass of gas at a constant volume, the pressure exerted by the gas is directly proportional to its absolute temperature.
(a constant)
******image *******
As temperature increases, the mean kinetic energy and thus the mean speed of the particles increases.
This results in a greater change in momentum on impact with the walls of the container, so the force per unit area is greater, . As the volume remains constant, more frequent collisions also occur.
******image *******
Worked Example
Using the kinetic theory of gases, explain the effect of increasing temperature on the pressure.
Answer:
Increasing temperature causes the mean speed of the particles to increase; therefore, the change in momentum per collision increases, so so the force from each collision increases as shown by this equation,.
As the volume remains constant, there are more frequent collisions, resulting in increased pressure, since pressure is defined as force per unit area.
Worked Example
Using the kinetic theory of gases, explain the effect that reducing the volume has on pressure at constant temperature.
Answer:
This is Boyle's law. As volume decreases, the pressure increases. As volume decreases, the particles have less distance to travel between collisions, so the time between collisions decreases. There are more frequent collisions. As force equals the rate of change in momentum, the force per unit area increases and thus the pressure increases.
Worked Example
A gas of and is compressed to a volume .
Calculate the new pressure.
By what factor will the volume change if the pressure is tripled?
Answer:
Because they are inversely proportional, according to Boyle's law, the new volume will be a third of the original volume.
Teacher Tips: In question one, we are assuming that the temperature remains constant and using Boyle's law, = a constant. We could also use their relationship to see that if the volume is dropped by a factor of five, the pressure will increase by a factor of five.
Worked Example
Show that the area under a graph represents work done.
Answer:
It is helpful to think of the units for pressure and volume:
Then multiplying them, because that’s how we calculate area under a graph:
We know that work done is measured in Newton-meters, so the area must be equal to the work done.
The ideal gas law equation
The three gas laws can be combined to form the ideal gas law equation.
Reminder: It is assumed in A-level Physics that you remember how to calculate moles from GCSE Chemistry, .
represents the mass, which in chemistry must be in grams, and RMM stands for the relative molecular mass. For example, for Carbon- has a RMM of .
We also know from GCSE chemistry that, .
represents the number of particles and represents the Avogadro constant ().
Worked Example
Calculate the pressure in a child’s helium balloon at degrees Celsius if it can be modelled as a sphere, radius , containing moles of helium gas.
Answer:
Plugging these values into the ideal gas equation, gives:
Teacher Tips: We use the volume of a sphere, remembering to convert from centimetres to meters, and we recall that temperature must be in Kelvin for the equation to work.
Practice Questions
An sealed container of ideal gas, initially at is compressed to half its original volume, keeping temperature constant.
It is then cooled at constant volume until the pressure is restored to its initial value. Calculate the final temperature.
-> Check out Brook's video explanation for more help.
Answer:
Does this represent Boyle’s, Charles’s or the Pressure law?
-> Check out Brook's video explanation for more help.
Answer:
Pressure law.