Escape Velocity
Brook Edgar
Teacher

Explainer Video
Escape Velocity
The gravitational potential, , at a point is defined as the work done per unit mass to move from infinity to that point in the field. Therefore, the energy required to remove an object from the Earth's surface is the exact opposite; it is equal to the gravitational potential at the surface multiplied by the object's mass -> , as the gravitational potential infinitely far away is defined as zero.
If an object is projected from Earth's surface at a speed, , the object will only be completely removed from the gravitational pull of the Earth if its kinetic energy is greater than the energy required to remove it from the surface of the planet:
The minimum speed at which an object can be launched to escape the Earth's gravitational pull is known as the escape velocity, found by equating the two energies, .
Formula:
We can use this formula to calculate the escape velocity for an object on any body, not just the Earth, as long as the gravitational field strength and radius of the body are known.
For example, to calculate the escape velocity for the Moon, mass , radius , we know that the kinetic energy of the object must be greater than the gravitational potential energy to move from the surface of the moon to infinitely far away.
Remember: The actual escape velocity will be higher than we have calculated, as we have ignored air resistance in our calculations. Although there is minimal atmosphere around some bodies, such as the moon, there will still be some resistive forces acting on the object.
Worked Example
Which Moon of Uranus has the highest escape velocity?
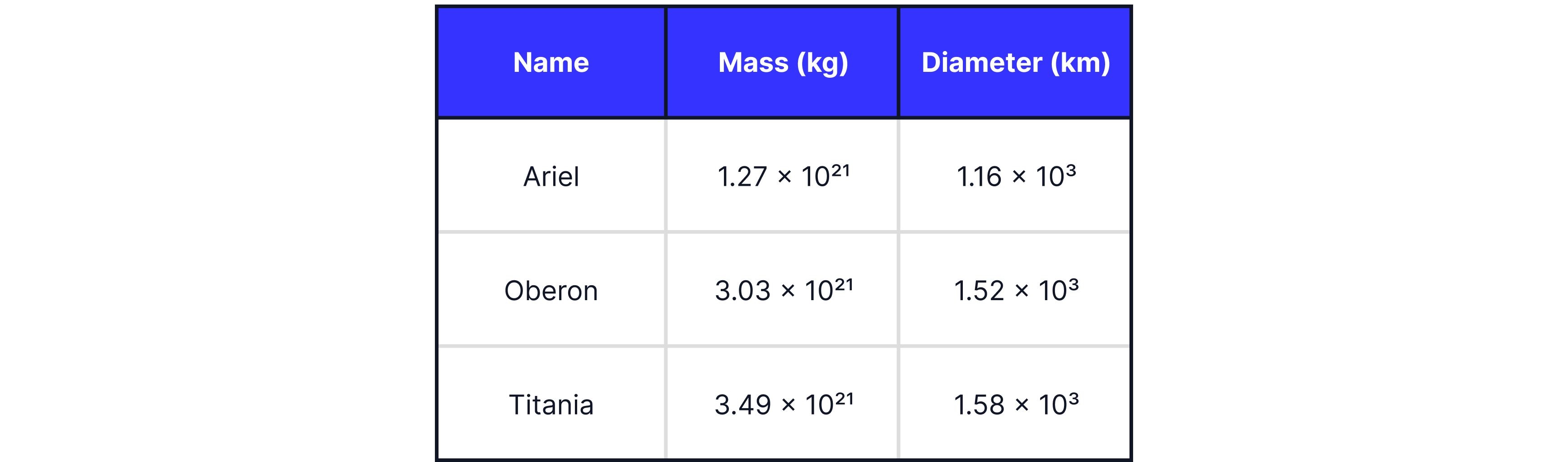
Answer:
We can simplify the relationship to understand escape velocity through proportionality:
-> as r is the radius of the body, in this case, the radius of a moon of Uranus.
As the diameter is equal to double the radius, we can then say, .
Therefore, the moon with the highest escape velocity will be the moon with the largest mass to diameter ratio:
Name | Mass () | Diameter () | Mass/Diameter () |
Ariel | |||
Oberon | |||
Titania |
-> Titania has the highest escape velocity.
Practice Questions
Describe how the concept of escape velocity is derived and calculate the escape velocity from the surface of the Moon.
Mass of the Moon
Radius of the Moon
-> Check out Brook's video explanation for more help.
Answer:
Kinetic energy must be greater than the gravitational potential energy required to escape the gravitational attraction from the planet/moon -> the energy required to move from the surface of the planet/moon to infinitely far away.
Calculate the change in gravitational potential energy needed for Earth to escape the attraction of the Sun.
Earth mass
Distance from Earth to Sun
Sun mass
-> Check out Brook's video explanation for more help.
Answer:
A meteorite hits Pluto and ejects rocks vertically at . Can these rocks escape Pluto?
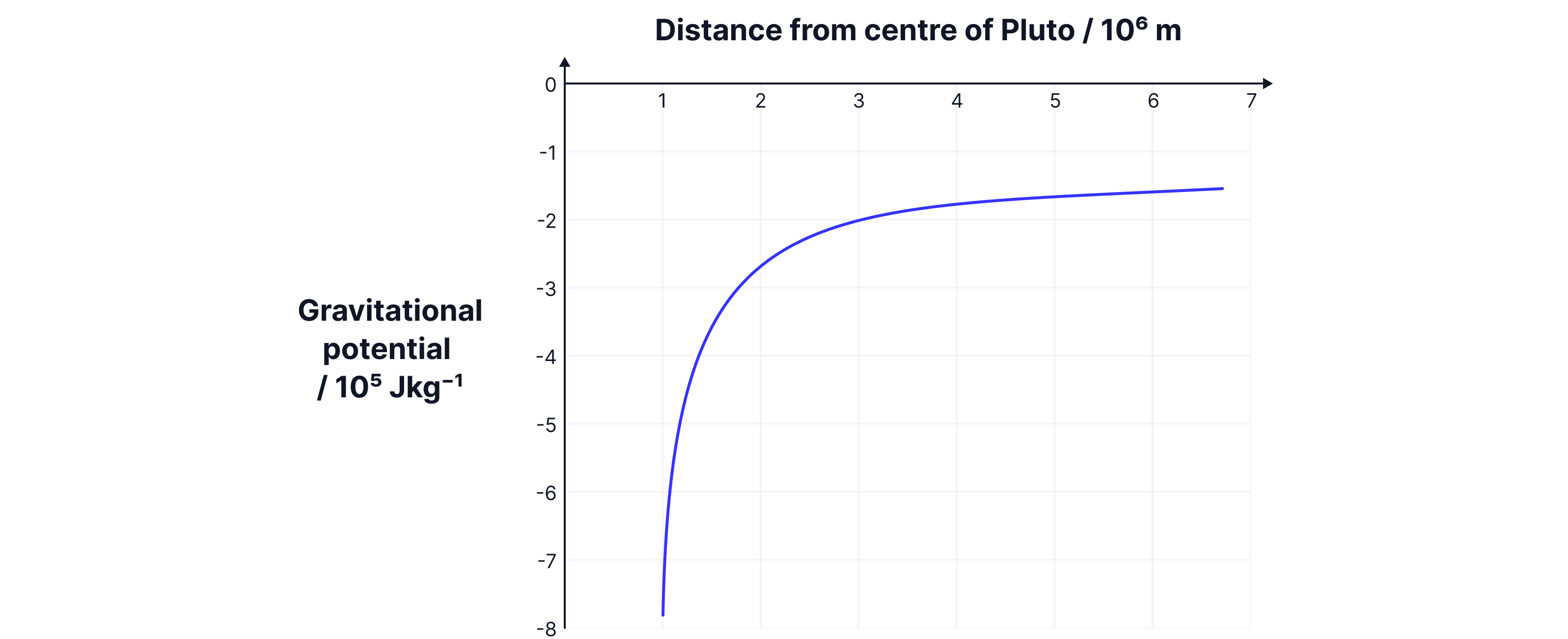
-> Check out Brook's video explanation for more help.
Answer:
Yes as .