If we know the pressure, volume, and number of particles of a substance, we can calculate the mean speed of the particles. Speed and temperature are directly related, meaning an increase in temperature corresponds to an increase in mean particle speed.

We can derive the kinetic theory model equation, by modelling a point particle, mass m and speed u, inside a cube container with sides of length .

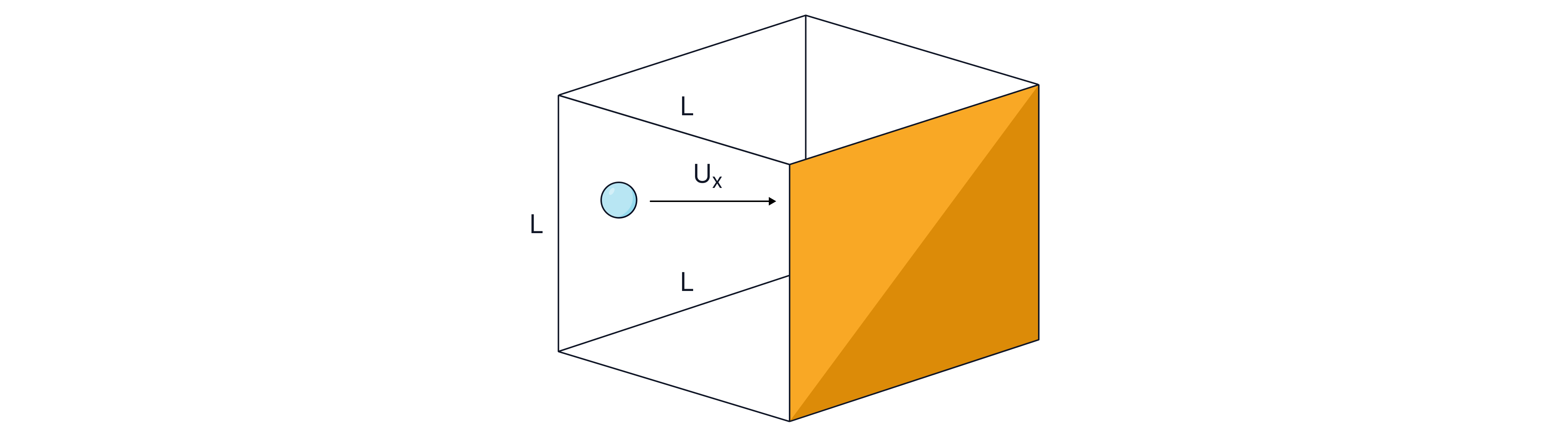
We begin the derivation by calculating the change in momentum of a particle when it rebounds from the wall of a container, as the collision is elastic only the direction changes:

initial momentum =

final momentum =

We know that force equals the rate of change of momentum, so combining our two equations:

We can substitute for time in the equation above knowing that the particle is travelling at speed , and that the distance the particle travels between collisions is (once the particle leaves the wall of the container, the yellow highlighted wall in the image above, it travels a distance to the other face of the cube and then back a distance ), .

Substituting time:

.

Knowing that pressure is force per unit area and that the area of the container, a square wall is we can now write:

As is volume the equation can be written, .

We have been modelling for one particle, moving in the direction, one third of space, and there are number of particles in the container. So the equation becomes:

.

We used to represent speed but not all particles are moving at the same speed, if we calculated the mean speed we would get zero (due to direction, the mean of and is zero) so instead we calculate mean square speed of particles, .

As mentioned, we use the root mean square speed of particles and not the mean speed, as the mean speed for a large number of particles would be zero, as they are moving in different directions (velocity is a vector).

To calculate the root mean square speed, we reverse the acronym, first square the speeds, calculate their mean and then take the square root of your answer.

For example, to calculate the root mean square speed of the particles below, we first square all of the speeds and then calculate their mean by dividing by five and then take the square root of the final answer.

Sometimes we can be asked to compare the kinetic energies of substances at the same temperature. The temperature of a substance tells us about its mean kinetic energy, so for substances at the same temperature, they have the same mean kinetic energy.

Formula:

Sometimes in exams, you are given molar mass rather than the mass of a particle/molecule. The molar mass is simply the mass of a single mole or particles (Avogadro's constant is the number of particles in one mole of a substance).

For example if we have a balloon of argon gas with molar mass, , at 300 K we can calculate the root mean square speed of the argon atoms in the balloon.

kinetic energy of an argon atom =

mole of argon atoms has a mass of ,

mass of 1 argon atom =