Moving Charges In A Magnetic Field
Brook Edgar
Teacher

Explainer Video
Moving Charges in Magnetic Fields
When a charged particle (like an electron or proton) moves through a magnetic field, the field interacts with the moving charge and exerts a force on it.
Formula:
The force on the charged particle is perpendicular to both its velocity, , and magnetic field, , causing the particle moves in a circular path.
The radius of a charged particle with mass in a uniform magnetic field is solved by equating the force on the charged particle due to the magnetic field to the centripetal force equation from the chapter on circular motion (paper 1).
The kinetic energy of a moving charged particle in a magnetic field remains constant. This is because the magnetic force acting on the particle is always perpendicular to its velocity. (In circular motion, the particle's velocity is tangential to the circular path, while the force points toward the center). Since the force and displacement are perpendicular, no work is done on the particle. As a result, the speed stays constant, although the direction of motion continuously changes.
Worked Example
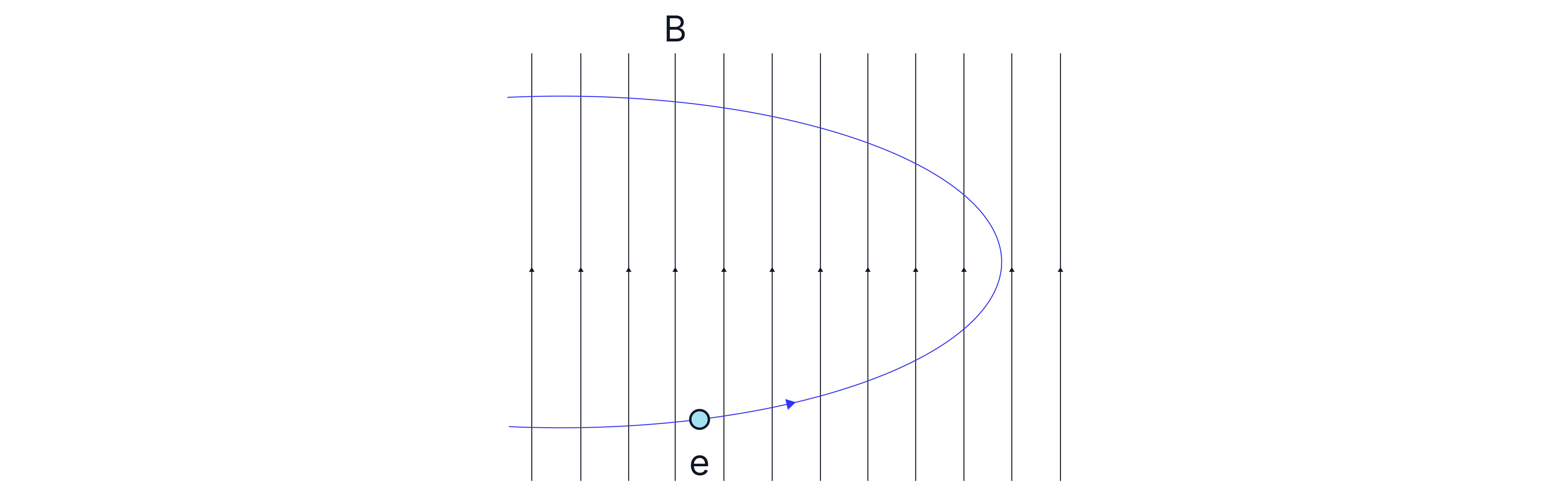
An electron enters a uniform magnetic field at heading downwards. The field's flux density is , and it is directed into the page.
Determine the direction of the force on the electron.
Calculate the magnitude of the force on the electron.
Describe the motion of the electron in the field. Support your answer with numbers.
Answer:
Using Fleming’s left-hand rule, the direction of the force is towards the left.
Remember: Conventional current is from positive to negative, so if the electron is moving down, the current is upwards.
Force is perpendicular to the electron's velocity, the electron moves in circular motion.
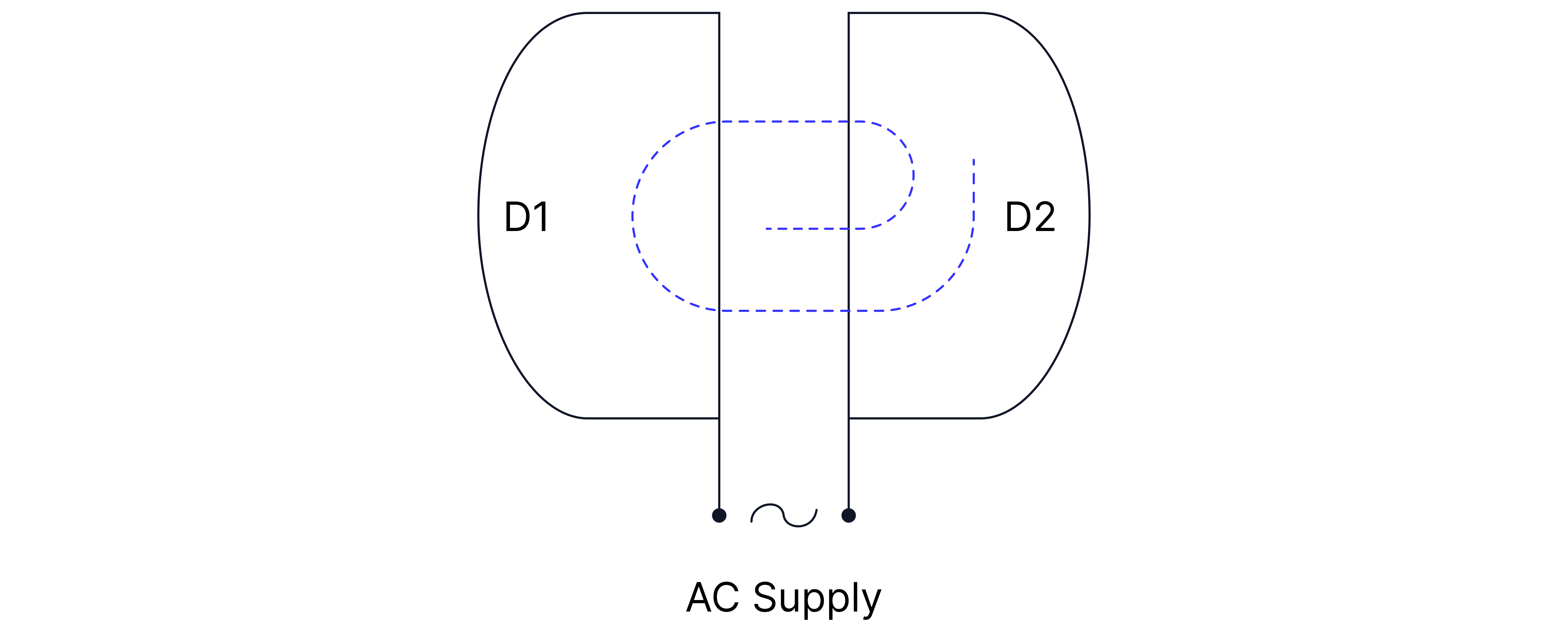
Cyclotrons
A cyclotron produces high-energy proton beams for radiation therapy. A cyclotron consists of two hollow, semi-circular metal electrodes called 'dees'. A uniform magnetic field is applied perpendicular to the plane of the dees. A high-frequency alternating voltage is applied between the dees, creating an electric field across the gap between them.
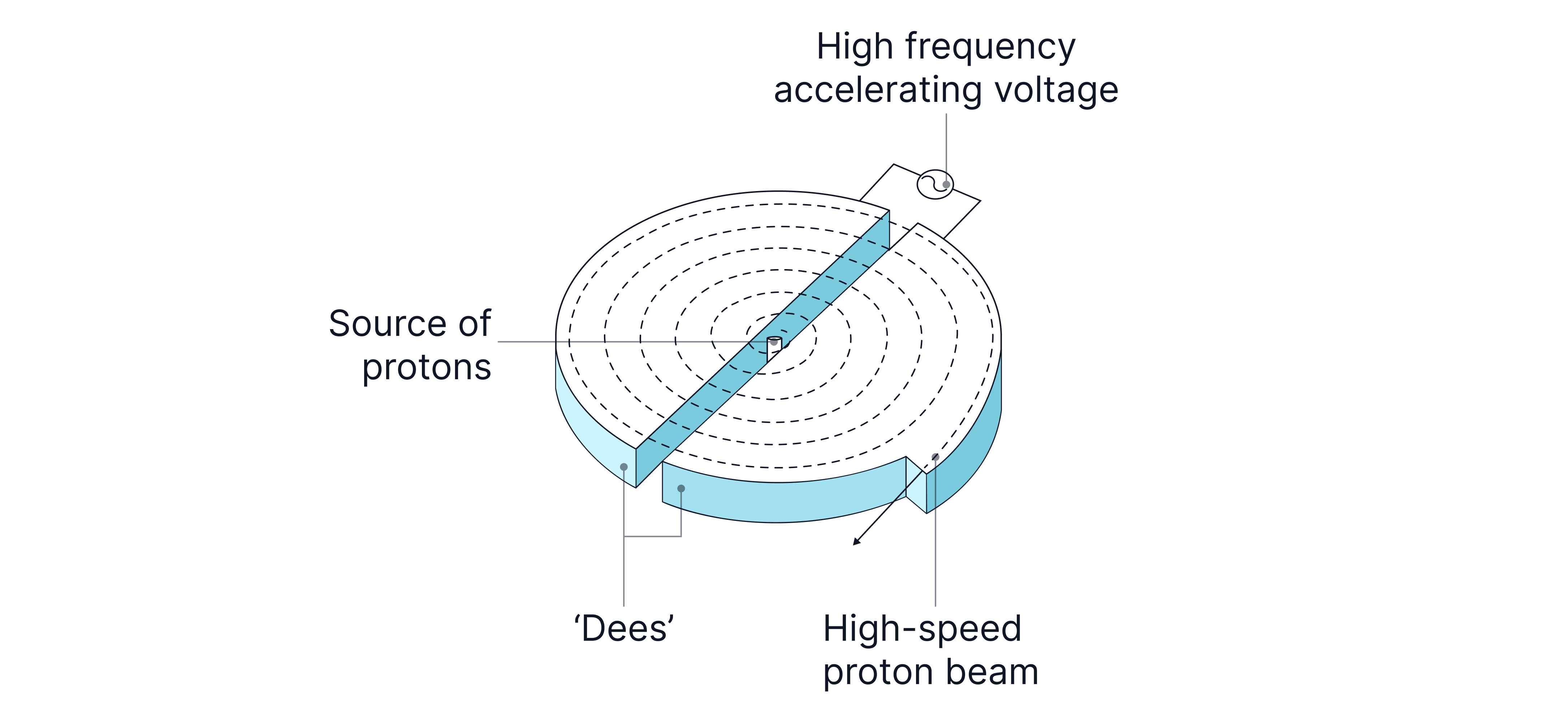
A charged particle (normally a proton) is injected into the centre and is attracted to the negative dee. The charged particle, now in motion, is forced into a circular path by the magnetic field inside the dee, which is oriented at right angles to the particle’s velocity. Each time the charged particle crosses the gap between the dees, it is accelerated by the electric field created by the alternating voltage.
The frequency of the alternating voltage remains constant, even though the particles are accelerated, because the time it takes for a particle to move in a semi-circular path within each dee does not depend on the particle's speed, as shown below:
The charged particle moves in a circle due to the force from the magnetic field in the dees.
Equate the two equations for velocities and rearrange for time:
The time period (therefore frequency) of a particle in a cyclotron does not depend on the radius of its circular path.
Worked Example
The first cyclotron, used to accelerate protons, was in diameter, with a magnetic flux density of .
Show that the protons emerged from the cyclotron at a maximum speed of
.
Calculate the maximum kinetic energy, in , of a proton from this accelerator.
Answer:
Teacher Tips: In question one, we used the charge of a proton as it is a proton inside the cyclotron. In question two, we use the mass of a proton, again, as it is a proton inside the cyclotron.
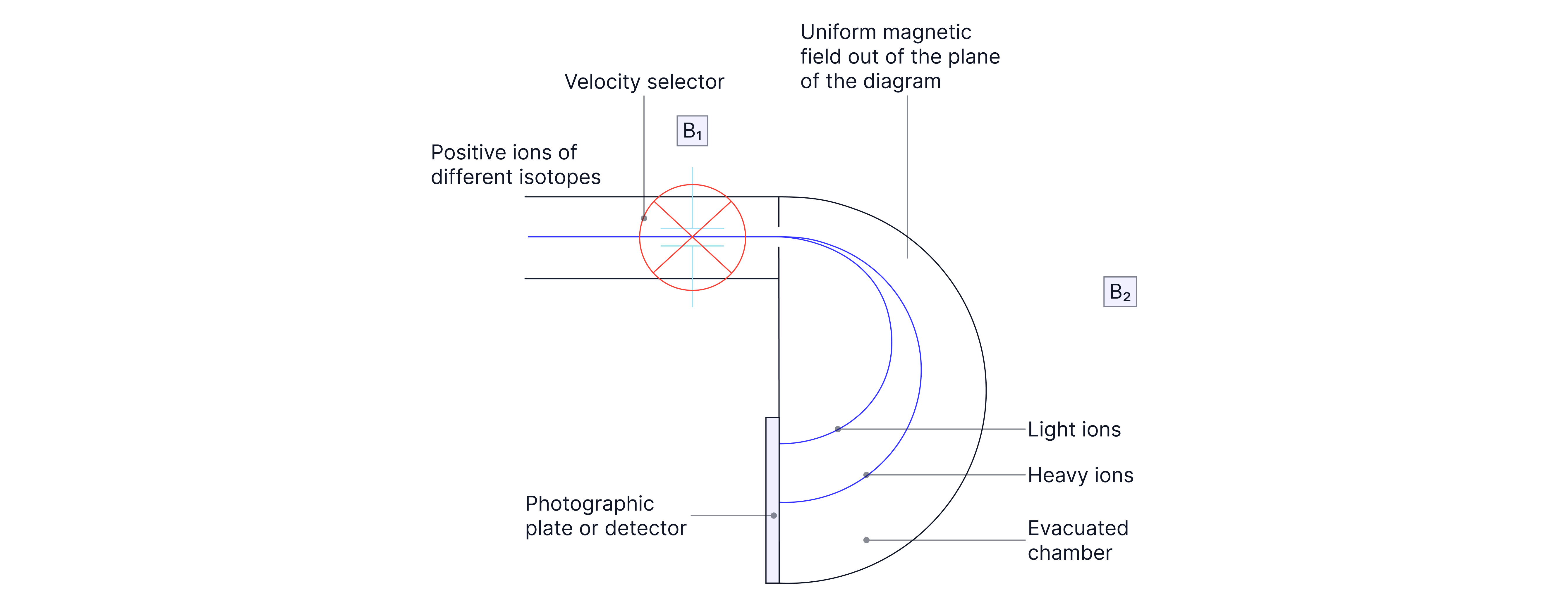
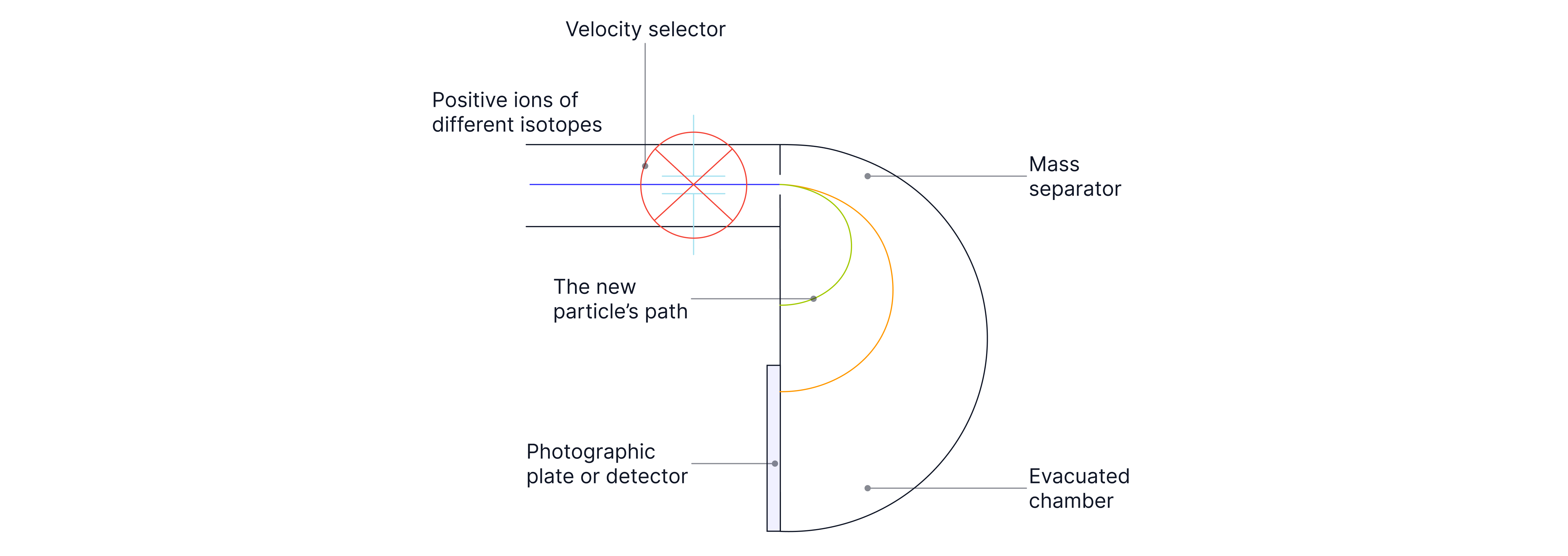
Mass Spectrometers
A mass spectrometer is used to analyse atoms in a sample. First, the atoms are all ionised and accelerated. They are directed into a velocity selector consisting of a magnetic field and a pair of plates at potential difference , , separation .
The ions experience two forces:
, due to the electric field.
, due to the magnetic field.
Ions moving at a speed where the two forces are equal, pass through undeflected into the uniform magnetic field region, where they are deflected by different amounts onto a detector. The amount they are deflected by depends on their specific charge. The detector then shows the relative abundance of each type of ion in the sample.
Worked Example
In a mass spectrometer, a beam of ions at a speed of are directed into a uniform magnetic field of flux density . An ion was deflected in a semi-circular path of diameter mm onto the detector. Calculate the specific charge of the ion.
A different type of ion was deflected onto the same detector when the magnetic flux density was changed to . This ion was deflected in a semi-circular path with a diameter of . Calculate the specific charge of this ion
Answer:
Teacher Tips: In question one, the ion moves in a circular path due to the magnetic field applied at right angles to its direction of motion. (paper 1). In question 2, the velocity selector ensures both ions enter at the same speed.
Worked Example:
An ion enters the mass separator with an equal mass but double the charge of the first ion. The path of the first ion is shown on the diagram. Explain and sketch the path of this new ion in the mass separator on the same diagram.
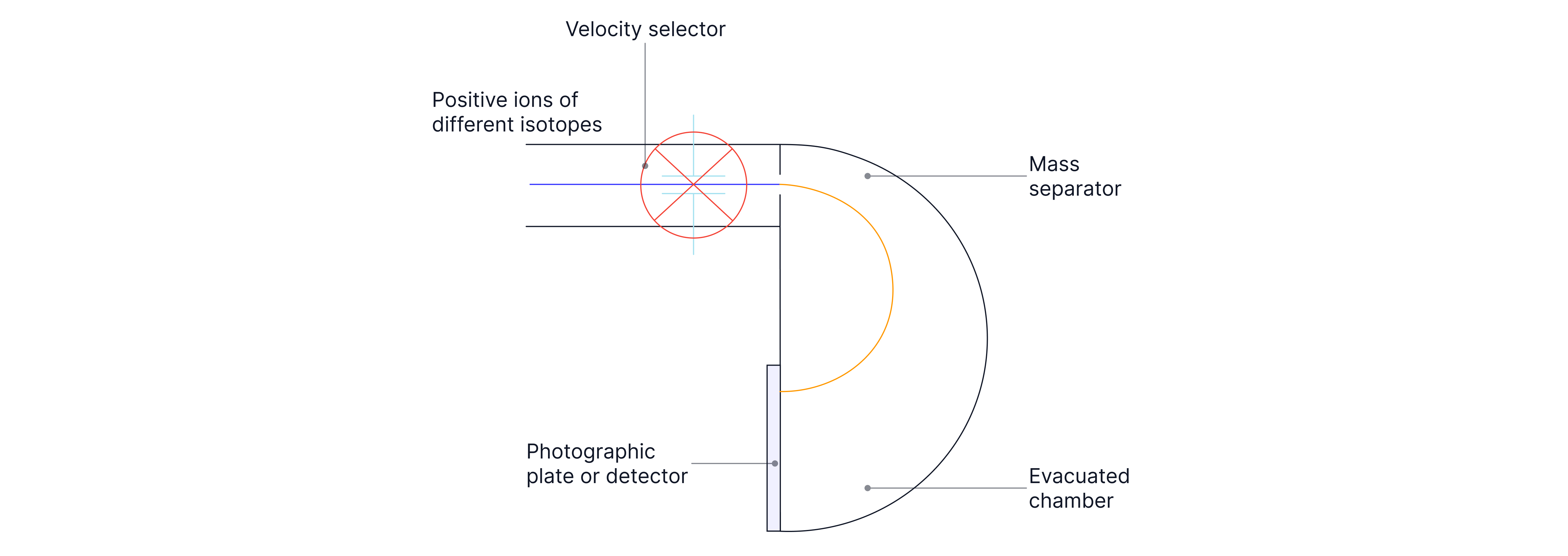
Answer:
Double the charge will half the radius, so half the diameter.
It will not hit the detector.
Practice Questions
A vertical magnetic field of flux density acts over the dees / into the page.
Explain why the proton travels in a semicircular path in a dee.
-> Check out Brook's video explanation for more help.
Answer:
The magnetic field is perpendicular to the velocity, causing a centripetal force on the proton, perpendicular to both its velocity and the applied magnetic field. This causes the proton to move in a circular path.
The peak potential difference applied across the dees is . The proton leaves the cyclotron with the kinetic energy of .
Determine the number of times the proton moved across the gap between the dees before it left the cyclotron.
-> Check out Brook's video explanation for more help.
Answer:
The proton crossed the gap times before leaving the cyclotron.