Probabilistic reasoning
Nick Featherstone
Teacher
Contents
Introduction - Probabilistic reasoning
What is probabilistic reasoning?
Assesses your ability to interpret and compare probabilities and percentages in given scenarios.
What is conditional probability?
Probability where the two events are dependent on each other.
E.g. If I am late for my bus I will be more likely to be late to school.
What are independent and dependent events?
Independent events - where one event is not affected by another event.
E.g. If I roll six on a dice, the likelihood of me rolling a three on my next roll is not affected by whether or not I roll a six on my first try.
Dependent events - when one event is impacted by another event happening.
E.g. Drawing two cards from a deck without replacing them.
What are mutually exclusive outcomes?
If two events are mutually exclusive, the occurrence of one automatically prevents the other from occurring.
E.g. In a single draw from a deck of cards:
Event A: Drawing a King
Event B: Drawing a Queen
You can’t draw a King and a Queen at the same time from one card draw - these events are mutually exclusive.
Why are probabilistic reasoning questions in the UCAT?
Questions reflect clinical decision-making, requiring weighing risks, interpreting test accuracy, and make safe judgements under pressure.
It tests conversion of fractions, percentages and frequencies into meaningful risk statements.
Explainer Video
Filmed by our Maths department, this video walks through how to solve Probability questions from first principles.
Worked Examples
Question 1 - Easy
Amy’s journey from home to school involves a short walk, a train from the station and an eight o’clock bus. If the train is late he will have to catch a later bus.
On 10 days out of the past 50, the train has not reached the station in time for him to catch the eight o’clock bus. Similarly on 10 days out of the past 50, the eight o’clock bus has arrived at Amy’s home station.
It is more likely than not that Amy will get home on time tomorrow?
A. Yes, the buses and trains each meet the requirements of the timetable 40 out of 50 times respectively, so she should get to school on time tomorrow.
B. Yes, if the train is late, the bus may be too, so she should get to school on time.
C. No, on 20 occasions over the 50 days either the train or bus has been late, so it is unlikely that she will get to school on time.
D. No, every day is different, so predictions are no more than guesses and wholly unreliable.
Answer
A. Yes, the buses and trains each meet the requirements of the timetable 40 out of 50 times respectively, so she should get to school on time tomorrow.
Worked Solution
Use a tree diagram to represent the probabilities.
Train is Late = 10 out of 50 = 10/50 = 0.2
Train is Not Late = 1 - 0.2 = 0.8
Bus is Late = 10 out of 50 = 10/50 = 0.2
Bus is Not Late = 1 - 0.2 = 0.8
E.g.
L = Late NL = Not Late B = Bus T = Train
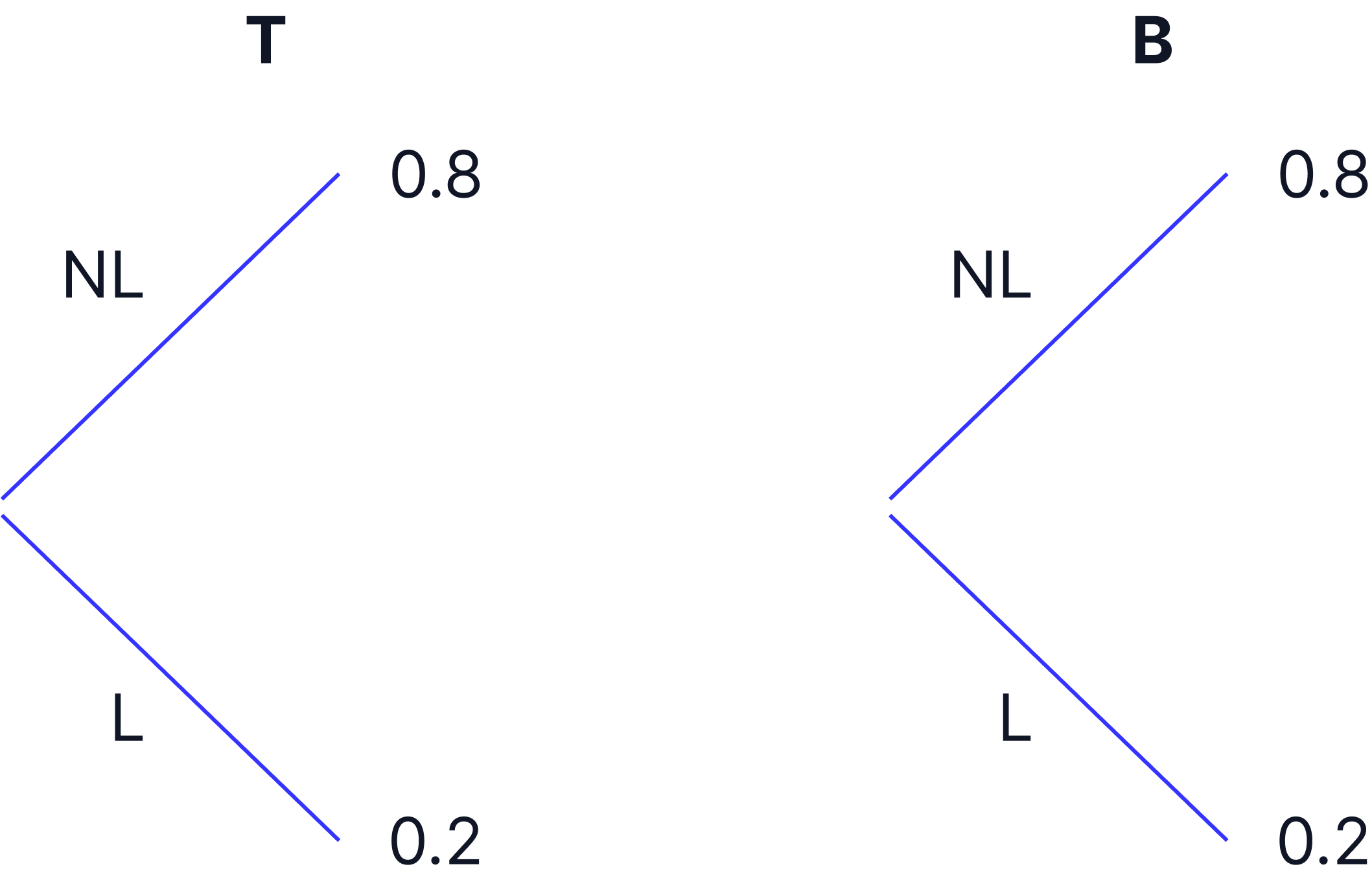
Probability On Time = 0.8 x 0.8 = 0.64
We multiply the probabilities because these are conditional probabilities.
Probability Late = 1 - 0.64 = 0.36
Therefore, the correct answer is A.
Question 2 - Medium
A company makes moisturiser.
The company carries out two opinion surveys, A and B, with different groups of people to test the quality of a new product.
200 people took survey A; 84 said they liked the product, 76 said they did not, the rest did not respond.
In survey B, 45% said they liked the product and 25% did not respond.
The company wants to use the survey that shows their product in its most favourable light. Should they choose survey A?
A. Yes, because the response rate in survey A was higher than that in survey B.
B. Yes, because a higher percentage of people in survey A than in survey B said they liked the product.
C. No, because the percentage of those who responded who liked the product was lower in survey A.
D. No, because the percentage of those who responded who liked the product was lower in survey B.
Answer
C. No, because the percentage of those who responded who liked the product was lower in survey A.
Worked Solution
Firstly, we must convert all the probabilities into decimals so that we are able to compare the probabilities:
‘200 people took survey A; 84 said they liked the product, 76 said they did not, the rest did not respond.’
Survey A
People who liked the product = 84/200 = 42/200 = 0.42
People who did not like the product = 76/200 = 38/100 = 0.38
People who did not respond = 1 - 0.42 - 0.38 = 0.2
‘In survey B, 45% said they liked the product and 25% did not respond.’
Survey B
People who liked the product = 45% = 0.45
People who did not like the product = 1 - 0.45 - 0.25 = 0.3
People who did not respond = 25% = 0.25
From our calculations, only statement C is correct.
Question 3 – Hard
Barry sells different sandwiches. Any sandwich can have up to 3 different fillings.
He decides to add an extra filling.
A. Yes, because there are 15 additional sandwiches from 4 + 6 + 4 + 1.
B. Yes, because there are 8 additional sandwiches from 14-6.
C. No, it will be 4 additional sandwiches as there are a total of 4 sandwiches
D. No, there will be 7 additional dishes from 3 + 3 + 1.
Answer
D. No, there will be 7 additional dishes from 3 + 3 + 1.
Worked Solution
Let’s name the different sandwich fillings A, B and C.
Therefore the initial filling combinations would be:
A, B, C, AB, BC, AC and ABC (7 flavours).
Introducing the new filling D, the new filling combinations (up to 4 flavours) would now be:
D, DA, DB, DC, DAC, DAB and DBC = 7
A, B, C gives 3 new combinations , AB, AC, BC give 3 new combinations, plus the new filling itself.
Therefore, the correct answer is D.
Worked Examples Video