Circular Motion
Brook Edgar
Teacher

Explainer Video
Circular Motion
Circular motion is the motion of an object in a circular path. The speed stays the same, but the velocity is constantly changing as the direction of motion constantly changes. The object is therefore accelerating, as acceleration is equal to the rate of change of velocity. There must then be a resultant force on the object causing this acceleration. This resultant force always acts towards the centre of motion and is known as the centripetal force.
In Earth's orbit around the Sun, gravity provides the centripetal force; for a car turning a bend, it's provided by friction between the tires and the road.
Worked Example
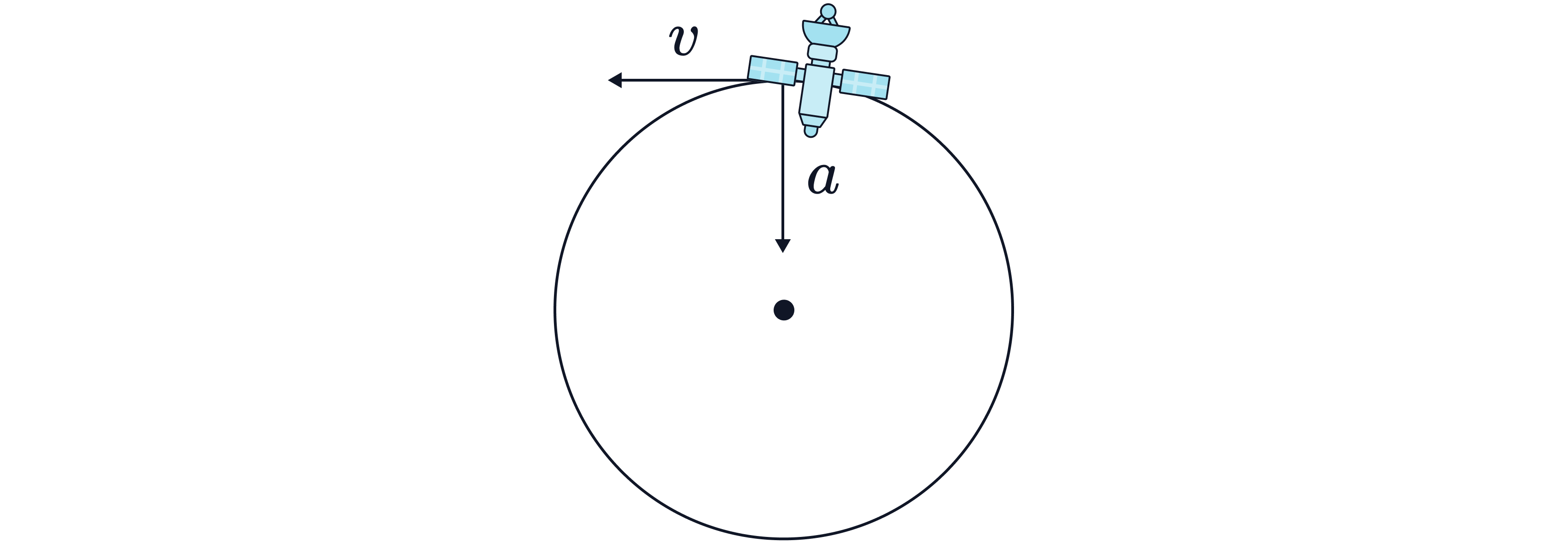
Explain why the kinetic energy of the satellite in orbit around the Earth does not change.
Answer:
Kinetic energy is constant as there is no work done on the satellite by the centripetal force due to gravity. The centripetal force acts perpendicular to the satellite's velocity, so no work is done on the satellite.
Teacher tips: work done = force × parallel distance
As speed = distance time, for circular motion, the distance travelled in one complete rotation is the circumference of a circle, , so the equation becomes,
An object moving in circular motion sweeps out an angle in a time, .
Formula:
For circular motion,
For example, if the mass of a ride is and the radius of the circular motion is , we can use , to calculate the centripetal force acting on the person on the edge of the ride, knowing that the ride makes nine revolutions in one minute.

Time period, , is the time taken for one revolution. There are nine in one minute, sixty seconds so, one revolution = .
The image below shows a car going over a hill, radius .

is the reaction force – the upwards force acting at right angles to the surface.
We can use circular motion equations to determine the maximum speed a car can go over this hill, without losing contact with the ground.
Here the force of gravity is causing the centripetal force. As the car is moving in circular motion, we know there must be a resultant force acting towards the centre of the circle. Therefore, the downward force of gravity must be greater than the support force.
To find the maximum speed the car can travel at without losing contact, we model for the situation when the car just loses contact with the ground. In this instance, the support force will fall to zero,
Now we have found the speed at which the car just loses contact with the ground. Therefore, the maximum speed a car can travel at without losing contact will be just below this number. Maximum speed that should not be travelled above = .
We can also apply circular motion to rollercoaster rides.
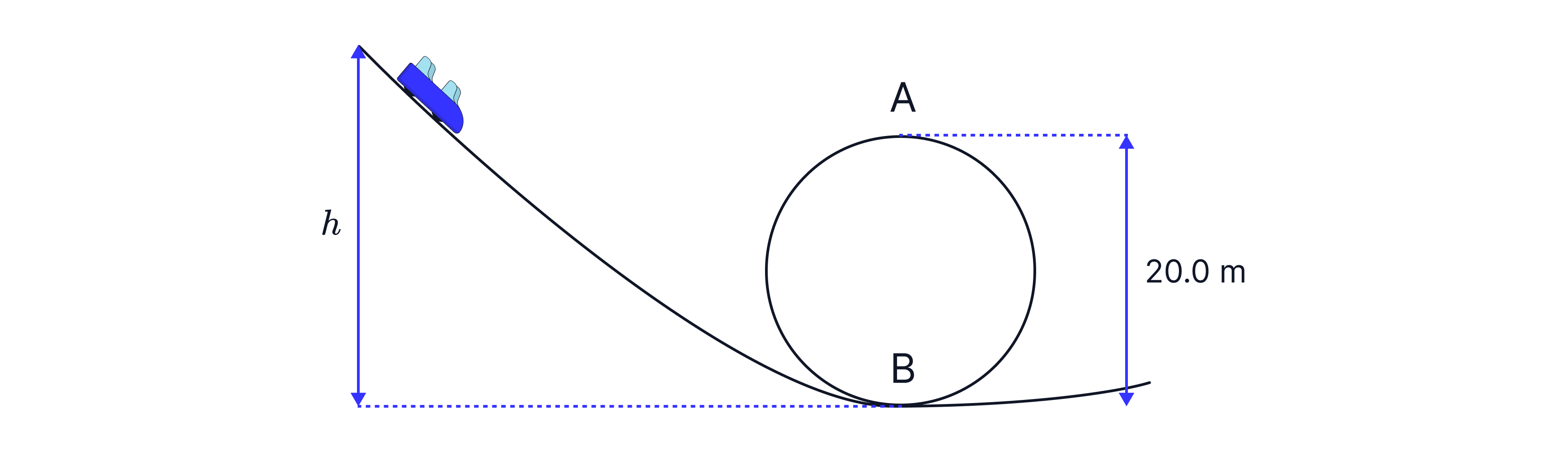
When the rollercoaster is at point A, both the weight and the support force act down, but at point B, they act in opposite directions.
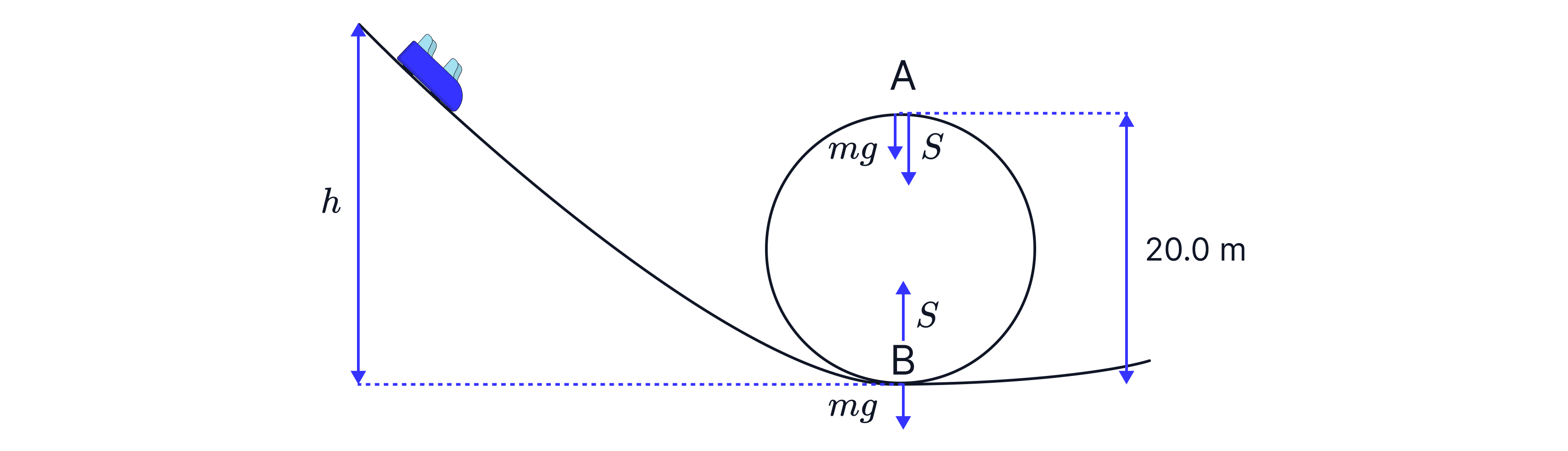
The support force is what you feel. We can use circular motion to prove that the person feels heaviest at the bottom of the loop.
At A,
At B,
The passenger feels the heaviest at B because the support force is larger here.
Teacher tips: In equation for A, adding mg will make S bigger. In the equation for B, subtracting mg will make S smaller.
Worked Example
A ball of mass , at the end of a string, length , is released from rest at point A. The ball swings in a circular path, passing through the lowest point B at speed . The tension in the string at point B is .
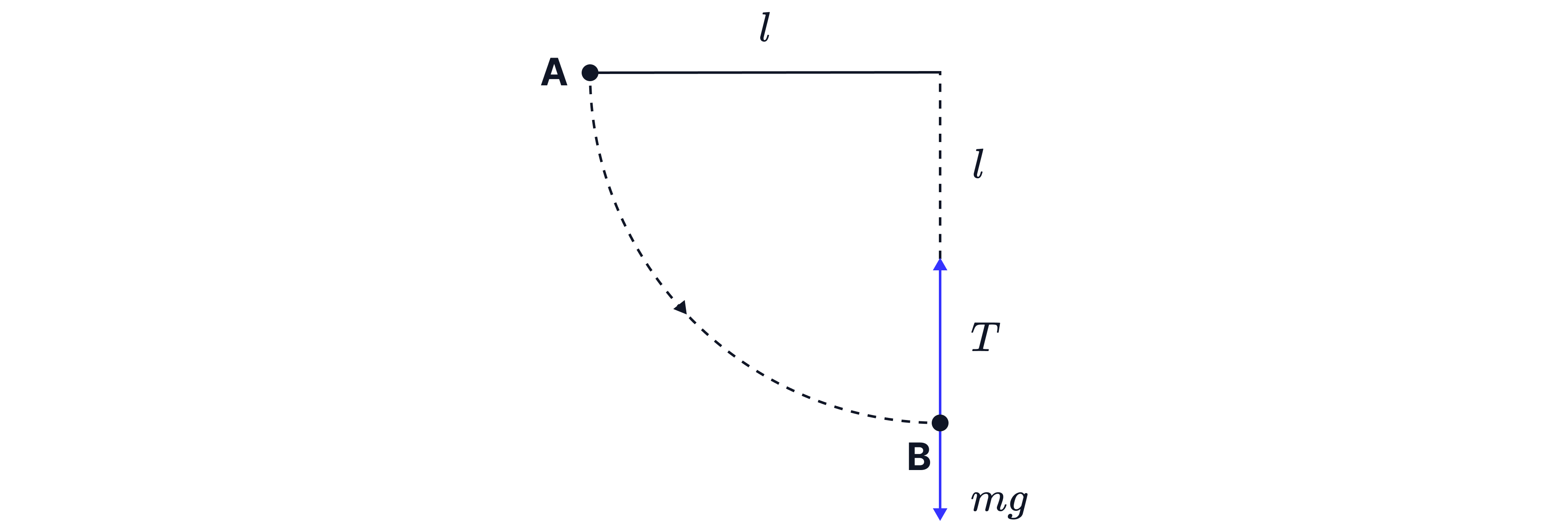
Which is correct?
A)
B)
C)
D)
Answer:
Since the ball is swinging in a circle, we know that , as there must be a resultant force (a larger force) towards the centre of the circle.
For circular motion,
The answer is C, as the radius of the circle is equal to the length of the string.
Practice Questions
The diagram below shows a rollercoaster approaching a loop. At height h it is stationary.
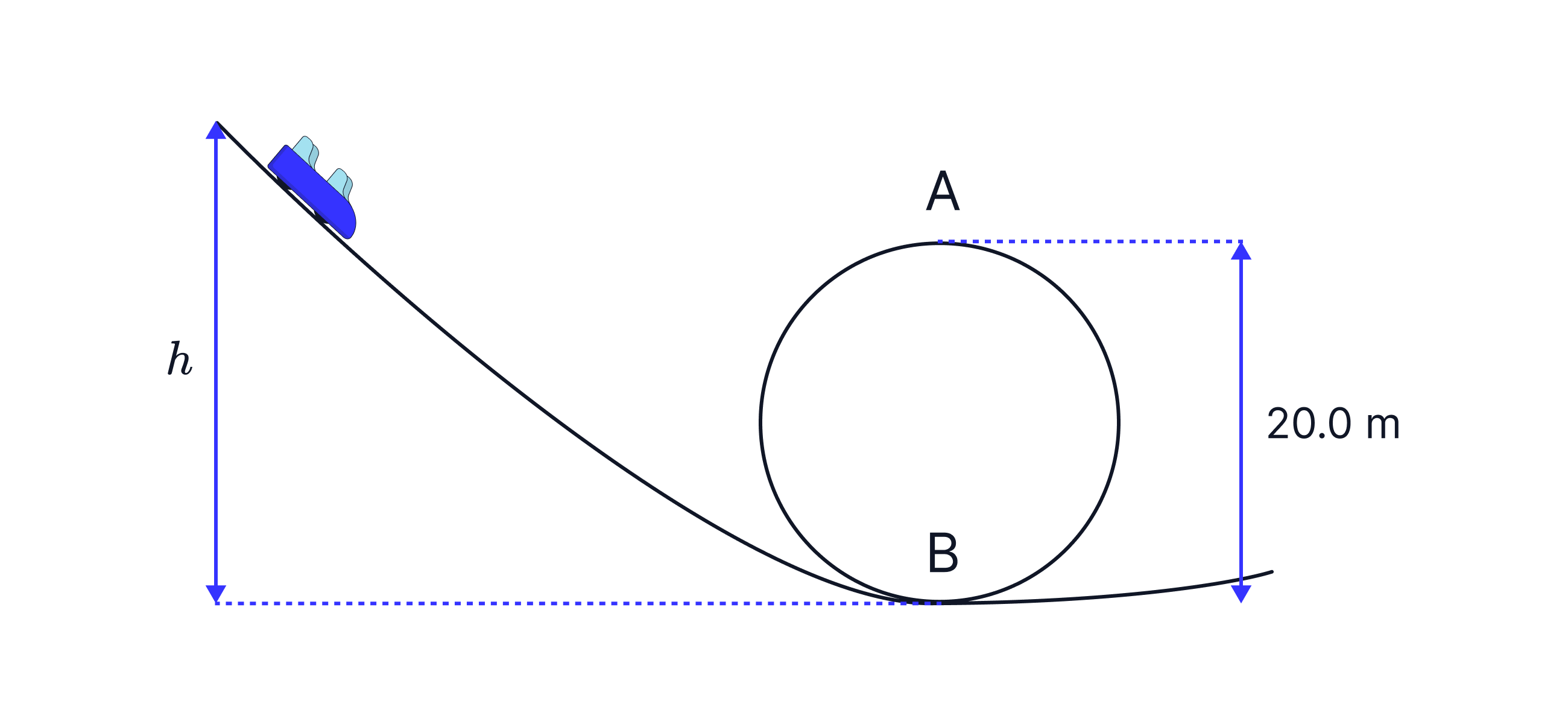
1) Draw a free body diagram at point A and point B.
2) Write two equations for the forces acting on the roller coaster car at points A and B.
3) Find the minimum height the rollercoaster must fall to complete the loop.
-> Check out Brook's video explanation for more help.
Answer:
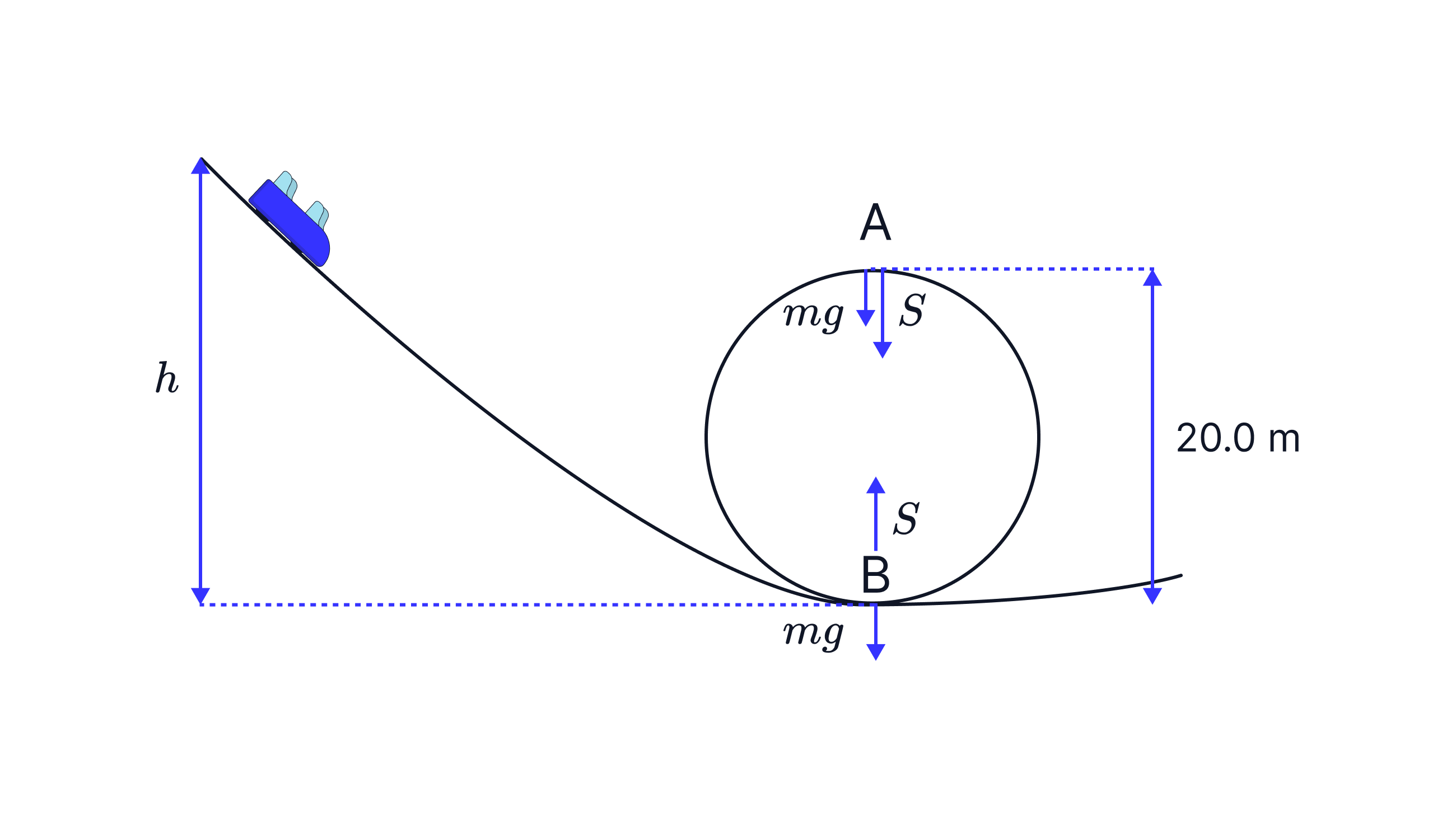
at A
at B
A mass rotates in a horizontal circular path of diameter . The rotation period is . The mass is and has a velocity of . Calculate the centripetal force on the mass.
-> Check out Brook's video explanation for more help.
Answer:
A plane flying as shown attempts to change direction at a constant speed of . Find the radius of curvature when the plane banks at an angle to the horizontal.
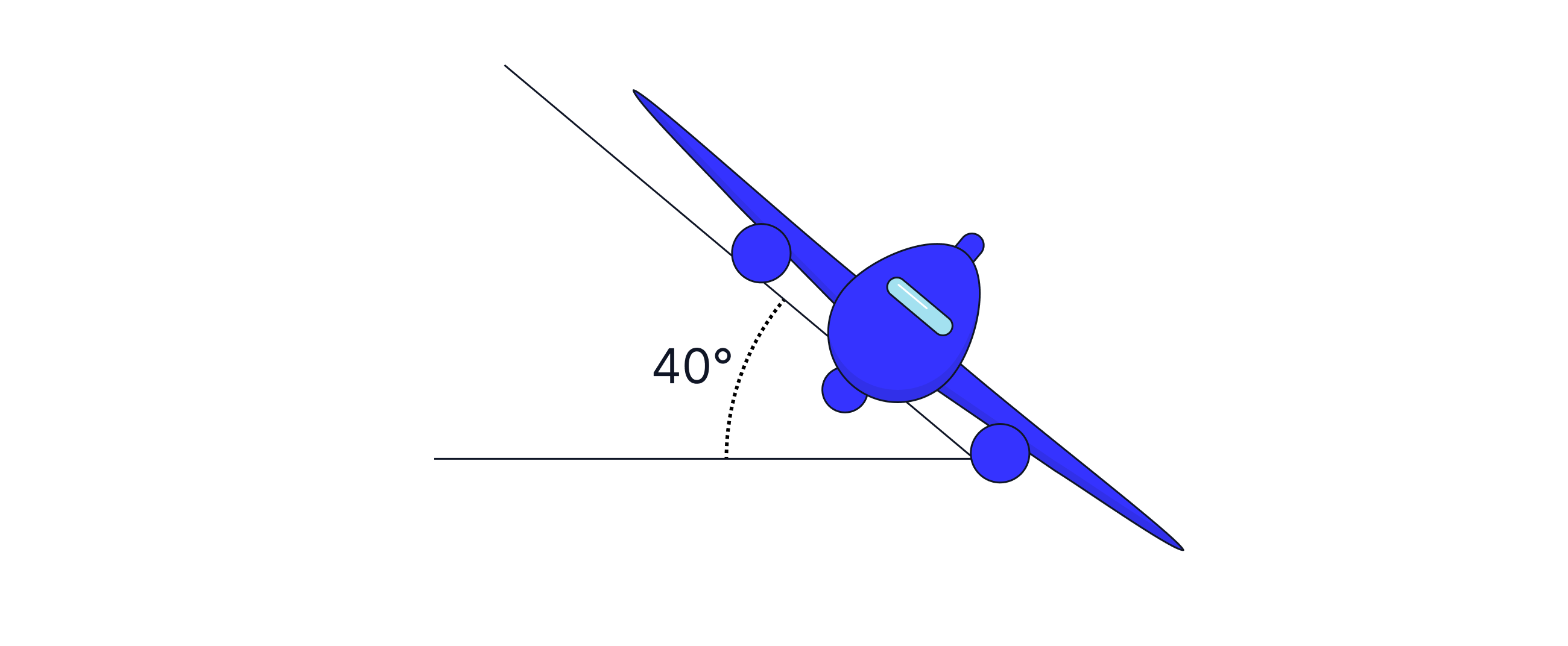
-> Check out Brook's video explanation for more help.
Answer:
On motorways the roads are sloped so cars are less likely to move out of their lane. The car has a mass of and is banked at , with a radius of . What speed signs are put up so friction down the slope is zero?
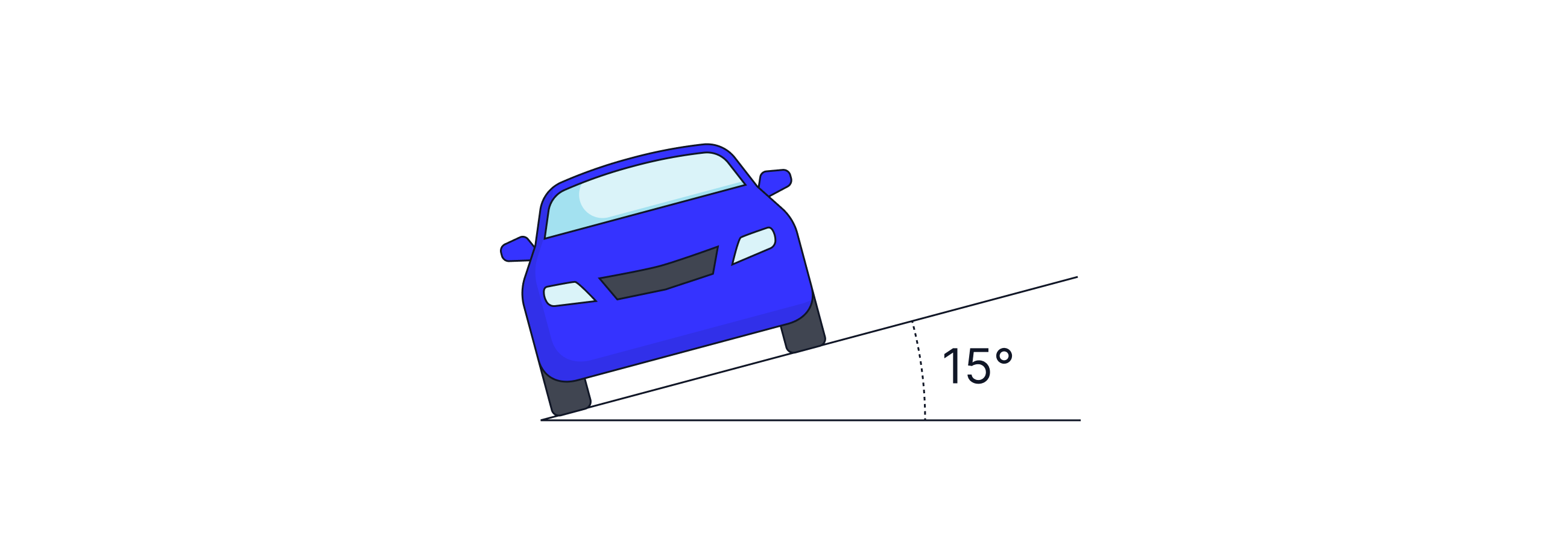
-> Check out Brook's video explanation for more help.
Answer: