Simple Harmonic Motion
Brook Edgar
Teacher

Explainer Video
Simple Harmonic Motion
Simple harmonic motion is a type of oscillatory motion where the:
Acceleration of an object is directly proportional to the displacement from the equilibrium.
Acceleration always acts towards the equilibrium position (i.e. it is a restoring force).
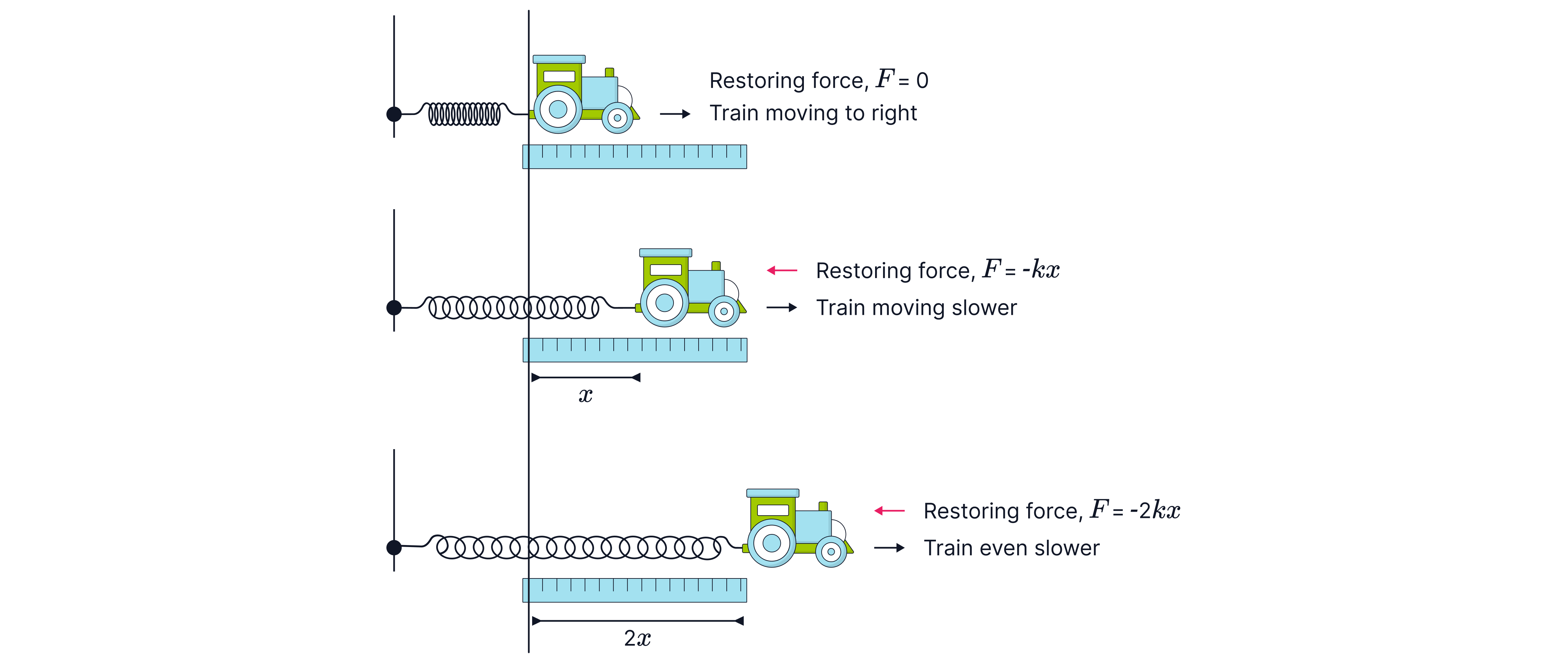
We can see that when the toy train is in its equilibrium position, , there is no acceleration or restoring force acting on the train. When the train is moved away from its equilibrium position, a force acts to pull the train back to its equilibrium position, a restoring force, proportional to the acceleration (). When the displacement is doubled, the restoring force and thus the acceleration back towards the equilibrium position are doubled.
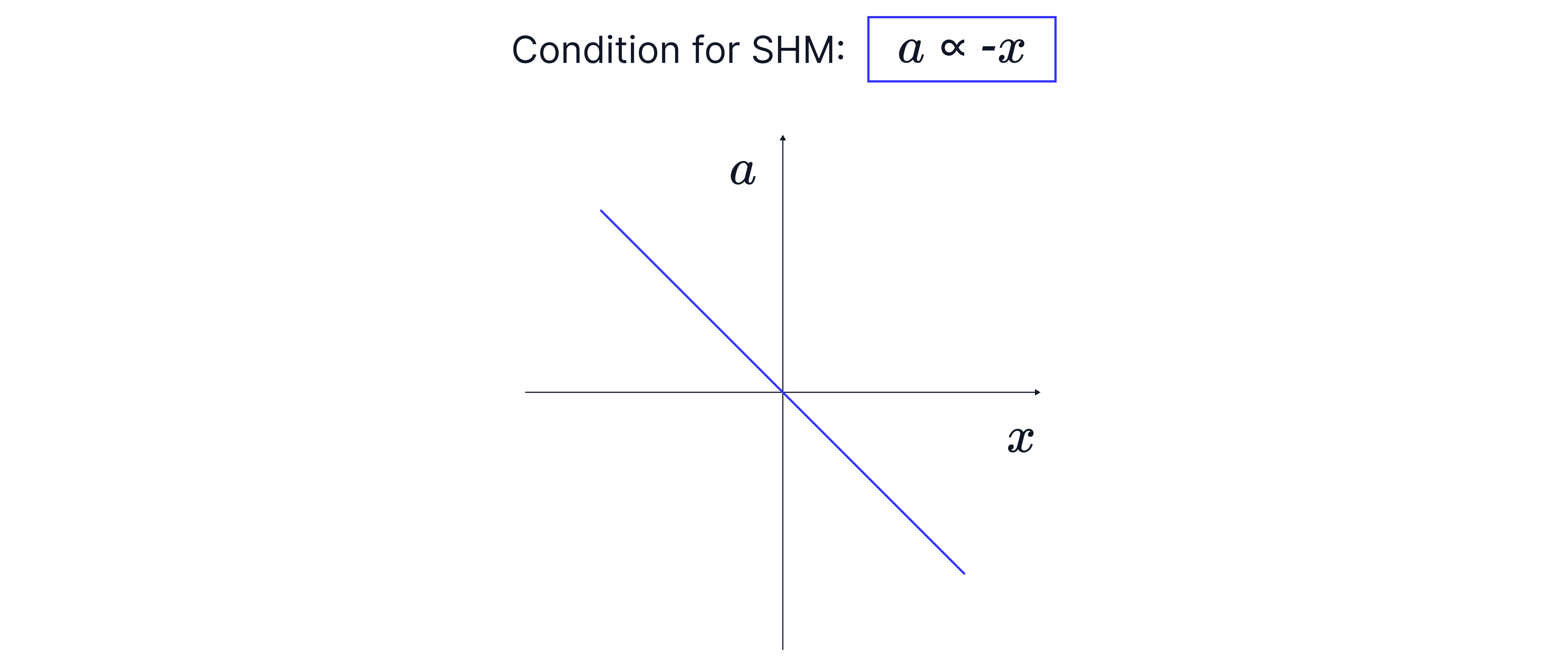
This equation can be written mathematically as, .
Formula:
Mass-spring systems undergo simple harmonic motion.
Formula:
From circular motion, we know that
∴
Pendulums also undergo simple harmonic motion.
Formula:
Free Oscillations
Free oscillations occur when there are no external forces acting (eg no air resistance). The total energy is conserved. When a pendulum swings, gravitational potential energy is converted to kinetic energy and back again. In a mass-spring system, elastic potential energy is converted to kinetic energy and back again.

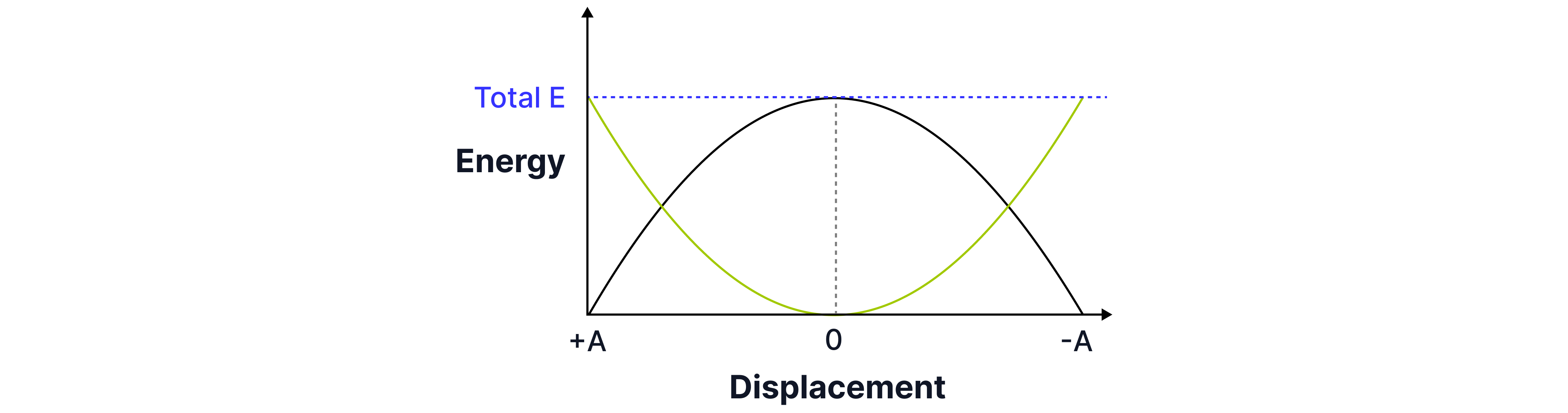
A pendulum is travelling fastest at its equilibrium position. Kinetic energy is at a maximum at the equilibrium position and at a minimum when the pendulum is at its maximum displacement from its equilibrium (at the amplitude, ). Kinetic energy is shown by the black line on the diagram below. The gravitational potential energy, then, is the opposite, shown by the green line below.
For a pendulum undergoing SHM, starting at its maximum displacement, its equation of motion can be written as, . At a time, , .
However, if the pendulum begins its motion at the equilibrium position its equation of motion becomes, . At a time, , .
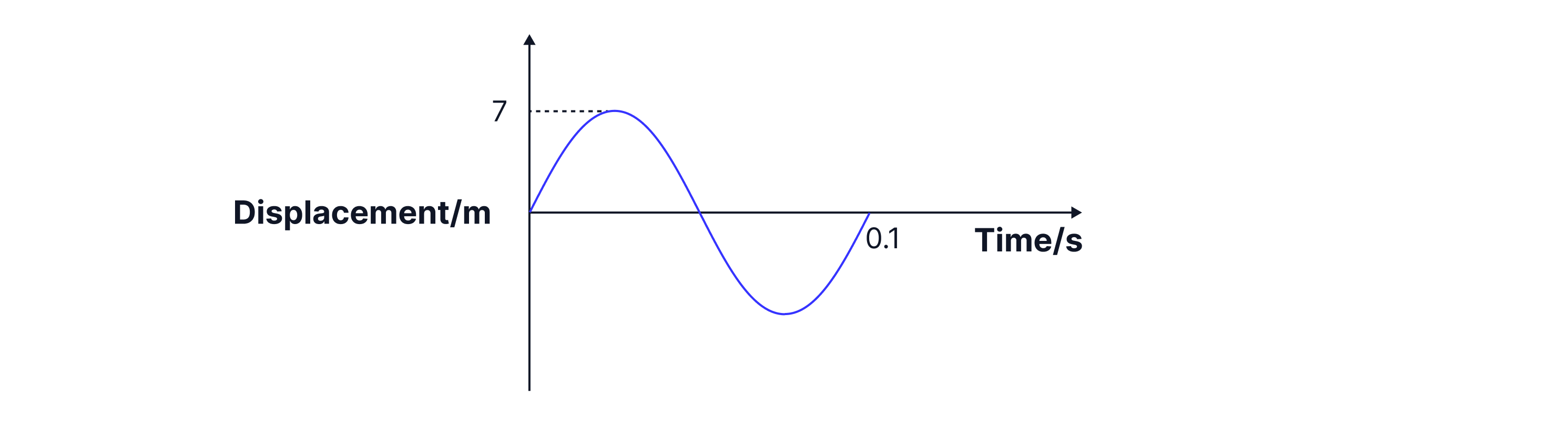
The diagram above is for a pendulum that starts at the equilibrium position with an amplitude of . The time period for the motion is .
The speed of the pendulum undergoing SHM can be written as,.
Maximum speed occurs at , therefore maximum speed, .
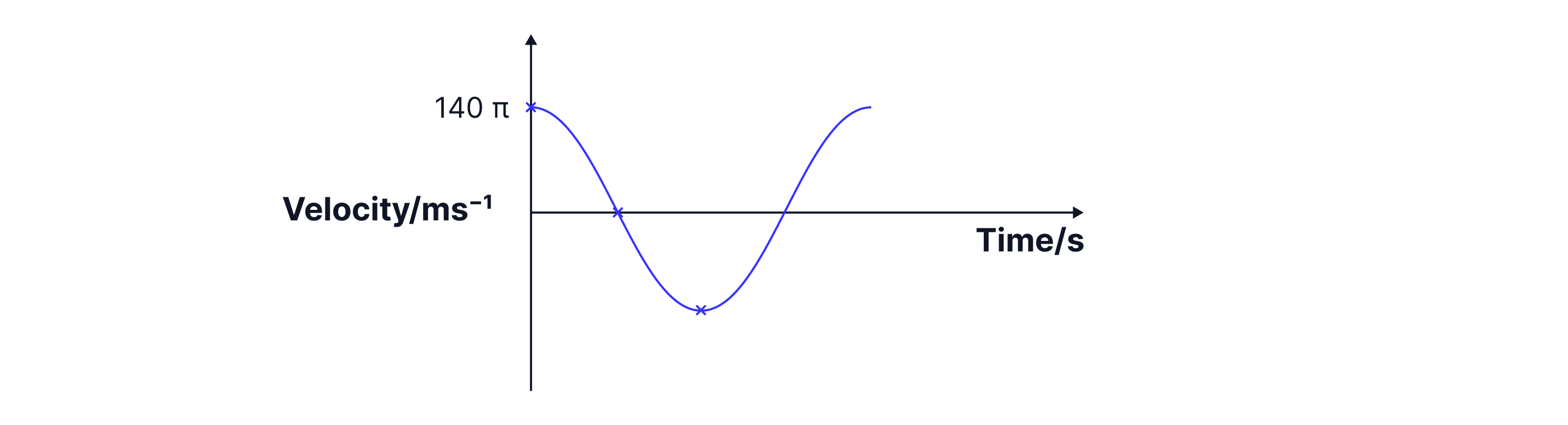
We can see that the v-t graph for the motion is, .
The acceleration is a maximum when the displacement is a maximum but in the opposite direction, . The curve of motion is therefore the negative of the s-t graph.
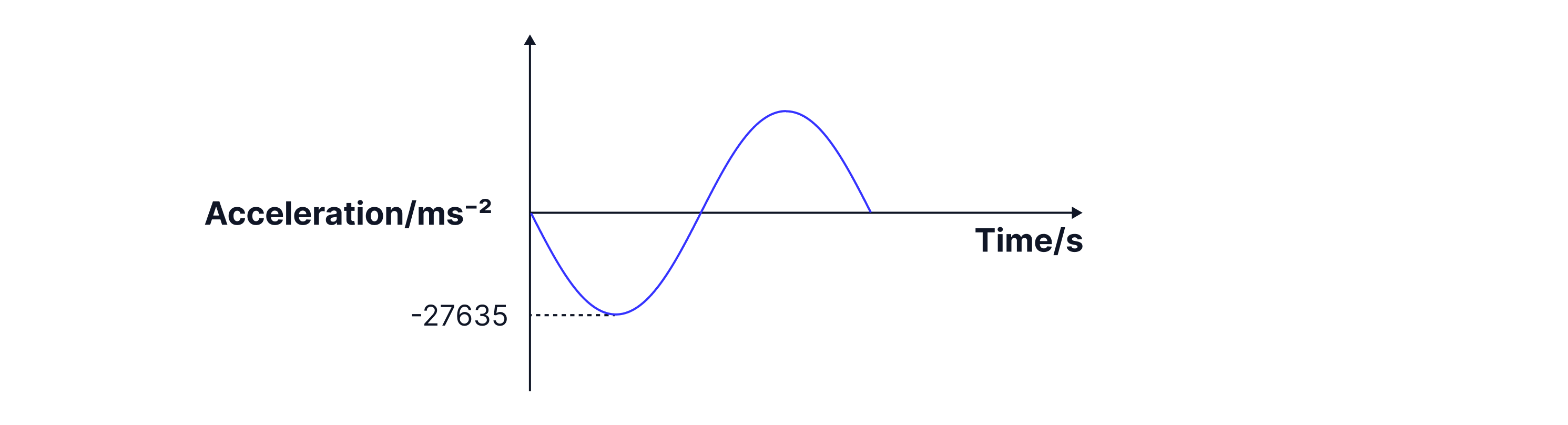
Worked Example
A pendulum oscillates with SHM at an amplitude of and a frequency of . Calculate the speed of the pendulum from the equilibrium.
Answer:
Worked Example
A mass on a horizontal spring is displaced and released from rest. The displacement of the mass is given by .
Calculate the maximum velocity of the mass.
Calculate the maximum acceleration of the mass?
Given the spring has a spring constant of , find the maximum kinetic energy of the mass spring system.
Answer
Comparing to the equation,, we can see that the amplitude is and that .
Kinetic energy is a maximum through the equilibrium position, when the elastic potential energy is a minimum. Therefore, by applying energy conservation, we can calculate the maximum elastic potential energy at maximum displacement and equate it to the maximum kinetic energy.
Practice Questions
The time period of oscillation of a pencil in water is given by:
If and the maximum displacement is, calculate the maximum acceleration.
-> Check out Brook's video explanation for more help.
Answer:
How long does it take the system to travel from the position of maximum displacement to the mean?
-> Check out Brook's video explanation for more help.
Answer: