Resonance
Brook Edgar
Teacher

Explainer Video
Damping
A system oscillating undamped will continue to oscillate forever at its maximum amplitude; however, in practice, there is always some energy loss over time due to resistive forces, such as friction or air resistance. This is known as damping. In light damping, the oscillations continue with a smaller and smaller amplitude, following an exponential decay, similar to a pendulum experiencing air resistance, such as a swing. The amplitude will decrease by the same fraction in equal time intervals.
Critical damping: The oscillator returns to its equilibrium position in the quickest possible time. Without overshooting/oscillating. An example of this is shock absorbers, e.g. the suspension in a car.
Overdamping/heavy damping: The system takes a very long time to return to its equilibrium position, and there are no oscillations. For example if a pendulum were oscillating and placed in thick honey. A real-life example would be a heavy door that closes slowly without slamming.
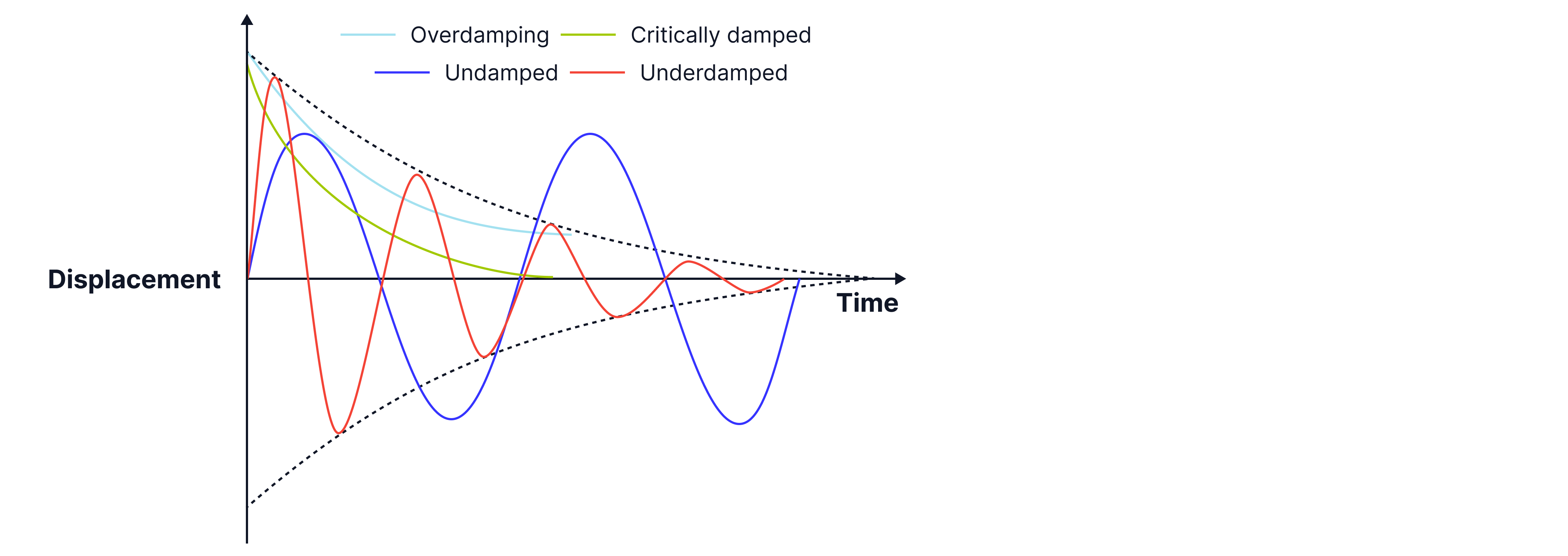
Remember: You need to be able to replicate this diagram.
Resonance
All oscillating systems have a natural frequency –> a frequency at which they naturally choose to oscillate at, when no external forces act.
A forced oscillation is when a system oscillates under the influence of an external periodic force (external driving force). The frequency at which the external force is applied to the system is referred to as the driving frequency.
If the driving frequency of the periodic force equals the natural frequency of the system, then resonance occurs. The amplitude of the oscillations increases drastically.
Resonance can cause systems to fail, which is why engineers must be aware of this phenomenon, as it can lead to glass shattering or the collapse of bridges. The Tacoma Narrows Bridge, located in the United States, opened in 1940 but closed a few months later due to resonance, as the wind hitting the bridge matched the bridge’s natural frequency, causing it to collapse.
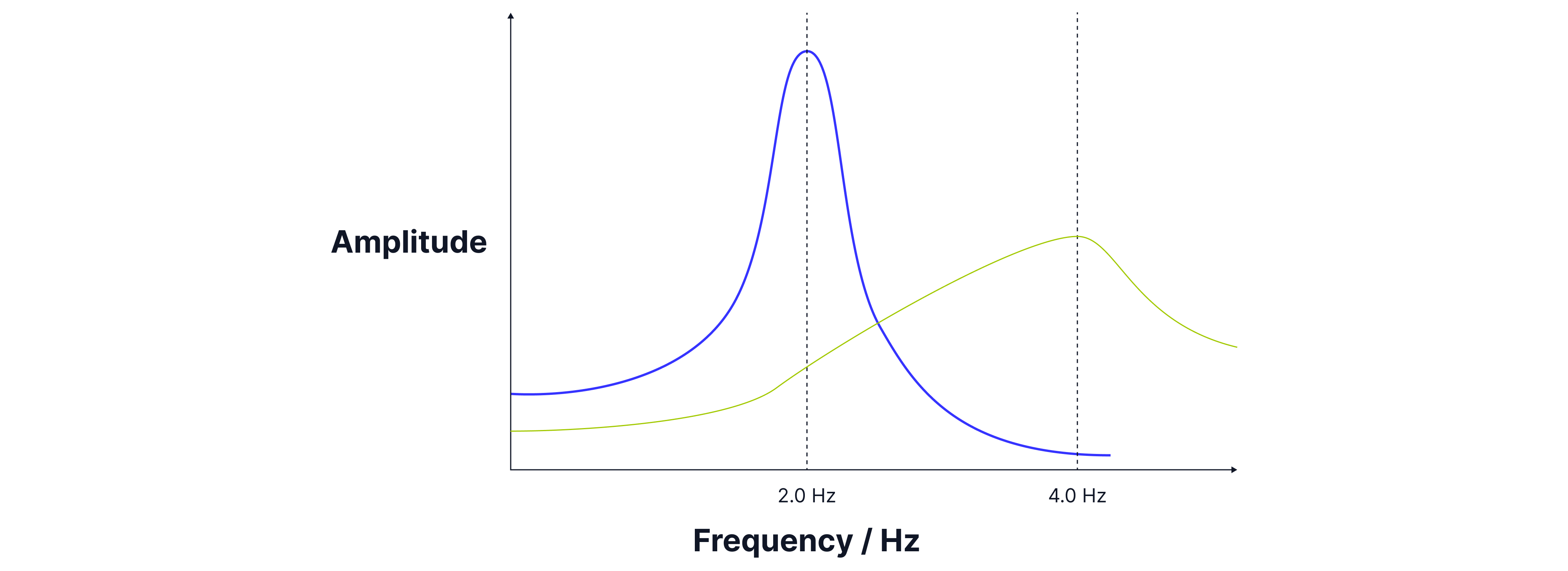
The graph below illustrates that as the driving frequency increases, the amplitude of oscillations increases, reaching a peak when the driving frequency matches the natural frequency. This is known as resonance.
When damping occurs:
The amplitude decreases at all frequencies.
The peak broadens.
The natural frequency decreases slightly - the peak shifts slightly to the left.
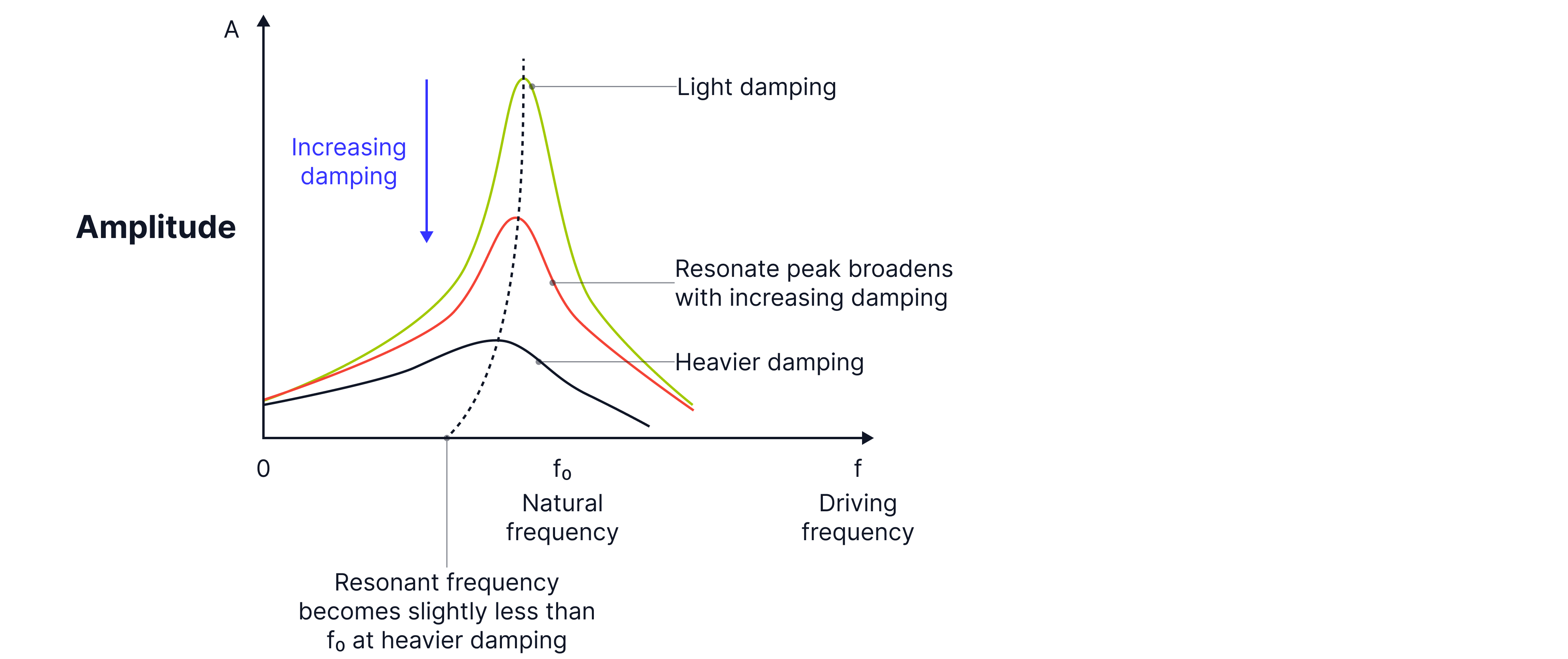
Remember: You need to be able to replicate this diagram.
Worked Example
The setup shown is used to investigate the effect of forced vibrations.
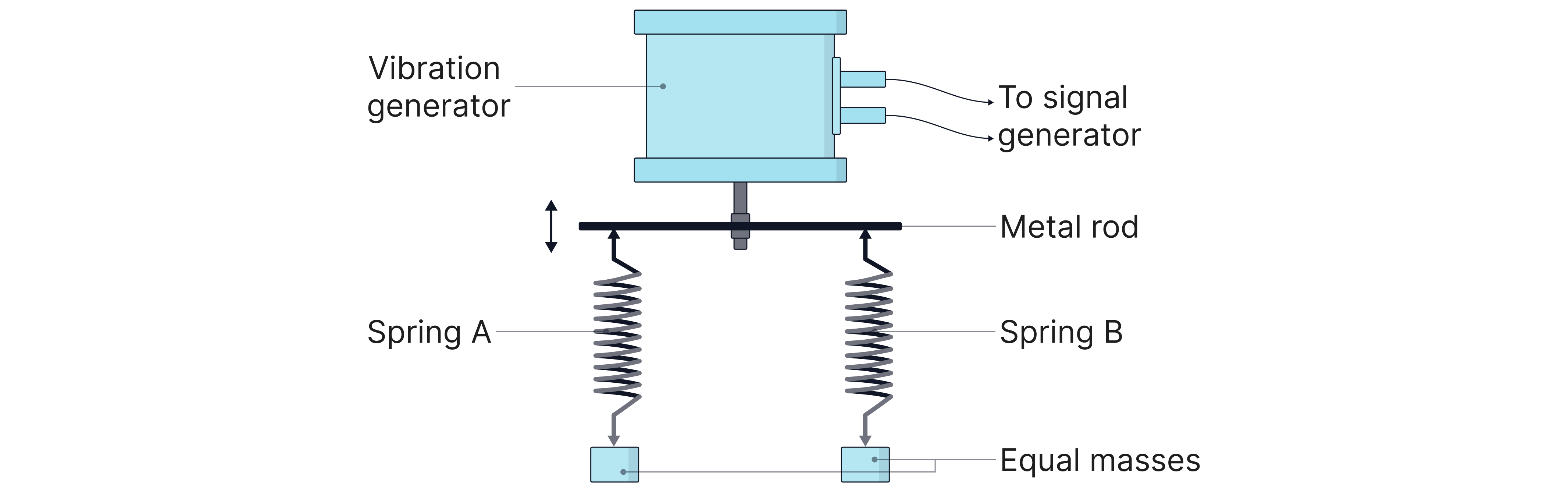
The stiffness of spring A is , and the stiffness of spring B is .
Two equal masses are suspended from the springs as shown.
When the signal generator causes the rod to vibrate at , the mass attached to spring A oscillates with a maximum amplitude of , with a maximum kinetic energy of .
Calculate the spring constant for spring A and the size of the mass.
Calculate the frequency at which the mass attached to B oscillates with maximum amplitude.
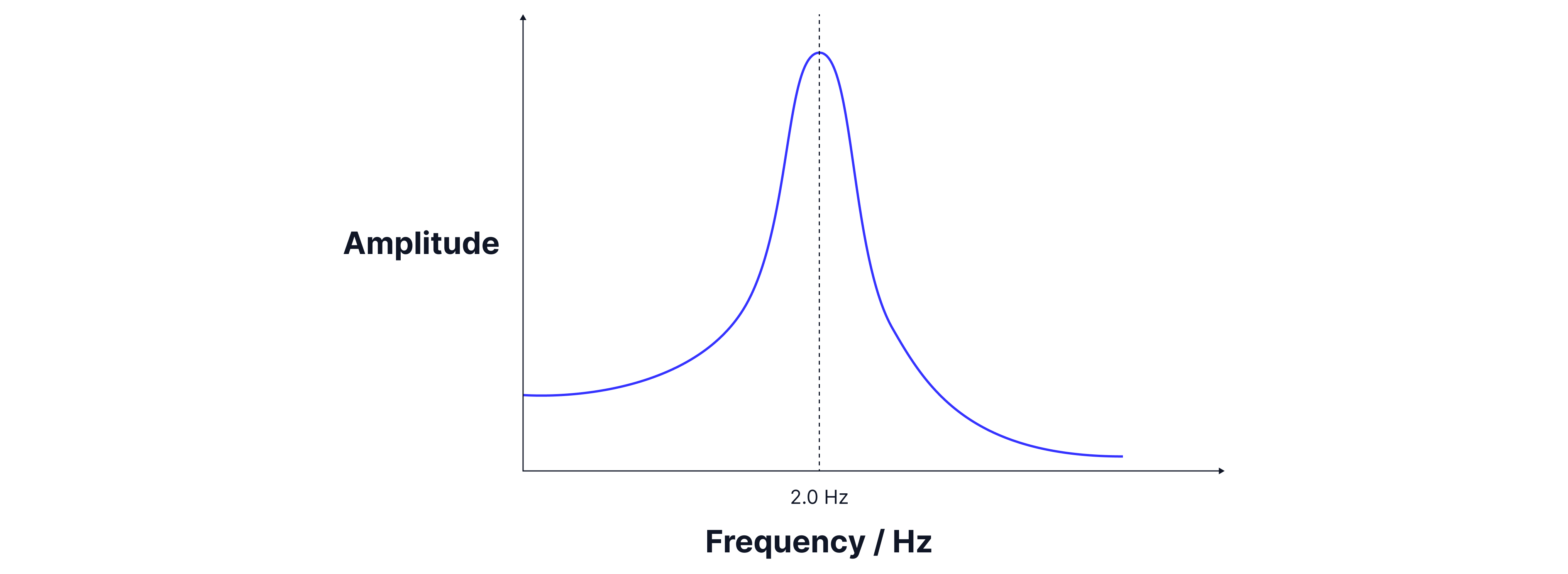
The graph below shows how the amplitude of vibrations varies for the mass attached to spring A. The investigation is repeated with the mass attached to B in oil. Explain how the graph would look different for spring B.
Answers:
We assume that energy is conserved. The maximum kinetic energy is equal to the maximum elastic potential energy, which occurs at maximum displacement -> the amplitude.
To solve for the mass, we use the equation for a mass-spring system,
For spring B, the spring constant is a factor of four greater, the time period will be changed by a factor of , as the mass is the same. The time period is reduced by a factor of two, and as , the frequency will be a factor of 2 greater = .
The natural frequency of B is , its peak amplitude will be at , but as it is in oil, it has been damped, the peak shifts slightly to the left of , and the amplitude of oscillations is lower at all frequencies, and the peak is broadened.
Practice Questions
A ship moves through continuous waves of wavelength and velocity at a steady speed of relative to the seabed. The natural frequency of heave oscillations in the ship is . A crew member needs an emergency operation, and it can be done if the ship is fairly steady.
Should they stop and anchor the ship or continue at ?
-> Check out Brook's video explanation for more help.
Answer:
Keep moving at as the applied frequency is much lower than the natural frequency.