Gravitational Field Strength
Brook Edgar
Teacher

Contents
Explainer Video
Gravitational Field Strength
Gravitational fields are regions around a mass where another mass will experience a force due to gravity.
Gravitational field strength is defined as force per unit mass.
Formula:
The gravitational force between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between the centres of the two objects, and is always attractive.
Formula:

Combining these two equations gives the gravitational field strength for a spherical mass, , at a distance :
We can see from the equation that the gravitational field strength from a spherical mass, such as a planet, follows the inverse square law.
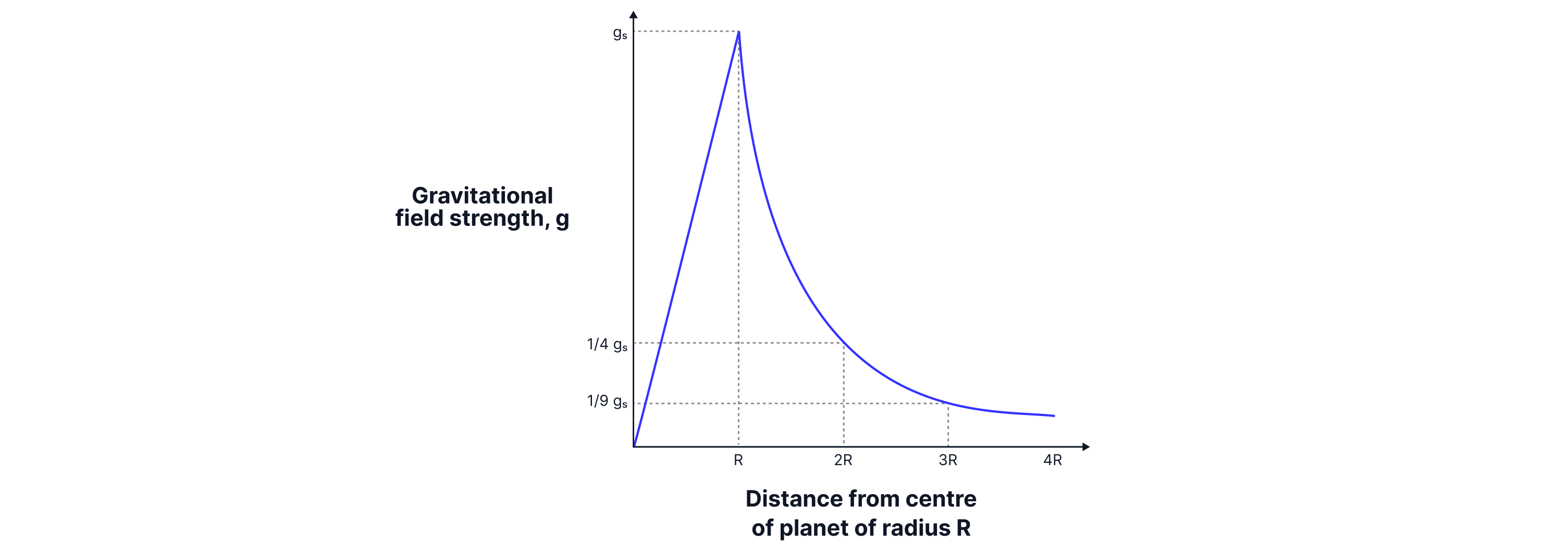
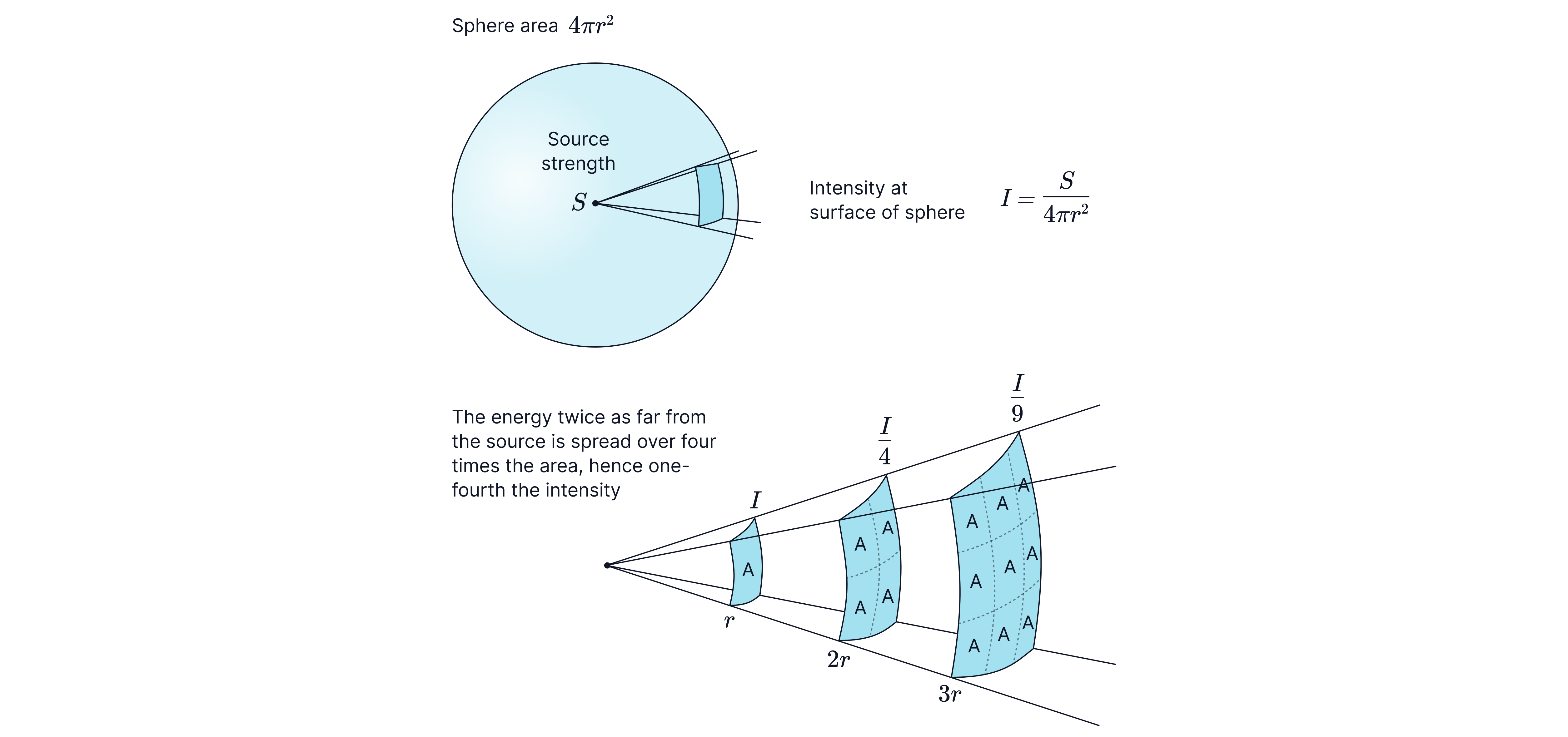
Remember: The inverse square law shows that as the distance increases, the intensity drops. The intensity is proportional to the reciprocal of the distance squared.
Gravitational field lines show the direction of the force that a unit mass would experience at each point in the field. Because gravity is attractive, the field lines around a point mass—or a spherical mass like Earth—always point inward, toward the centre. A unit mass placed near Earth would therefore feel a force pulling it toward Earth’s centre.
-> Field lines indicate the direction a point mass would accelerate if placed in that field.

As the Earth is so large, on the surface of the Earth up until around , the field lines can be modelled as uniform.

Worked Example
The centre of the Moon is from the centre of the Earth. The mass of the Moon is .
Calculate the force of gravity between the Moon and Earth.
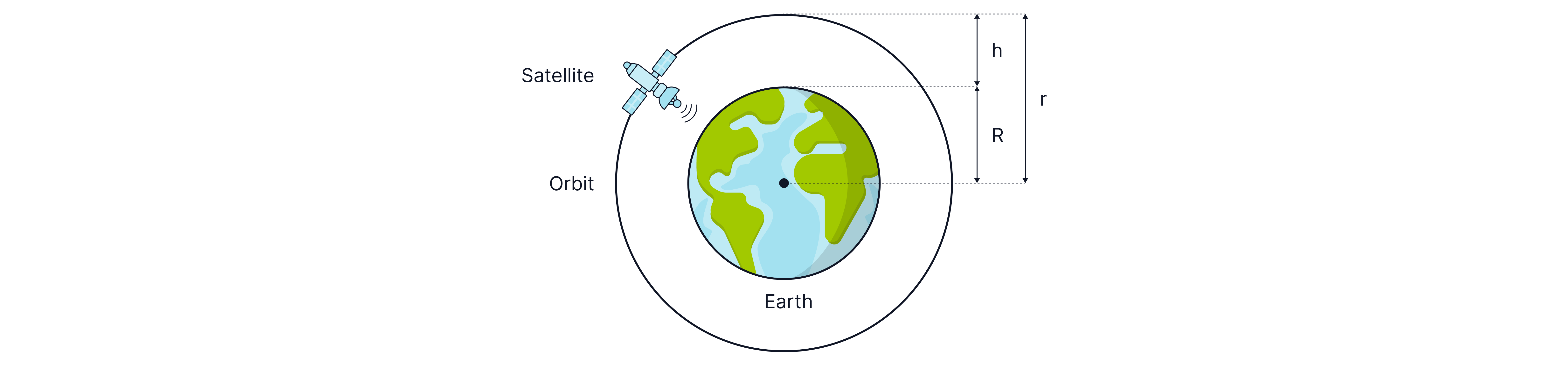
A mass of is placed at a point , which is from the centre of Earth as shown in the image below. Calculate the resultant force on this mass.

Answer:
Teacher Tips: The mass of the Earth, Sun and Radius of the Earth and Sun can be found on the AQA data sheet.
Orbits and Satellites
A satellite is kept in orbit around a planet due to the centripetal force of gravity between the satellite and the planet. The satellite does not crash into the planet as the direction of the centripetal force is perpendicular to the satellite's direction of motion (at a tangent to the circle).
The radius of a satellite's orbit is the sum of its height above the Earth's surface and the Earth's radius. The height is often referred to as altitude in exam questions.
From the circular motion topic we know that angular velocity, , for a full orbit/rotation, can be calculated as:
We can use this equation to calculate the size of the resultant force on the satellite:
or we can use the equation:
is the linear speed of the satellite.
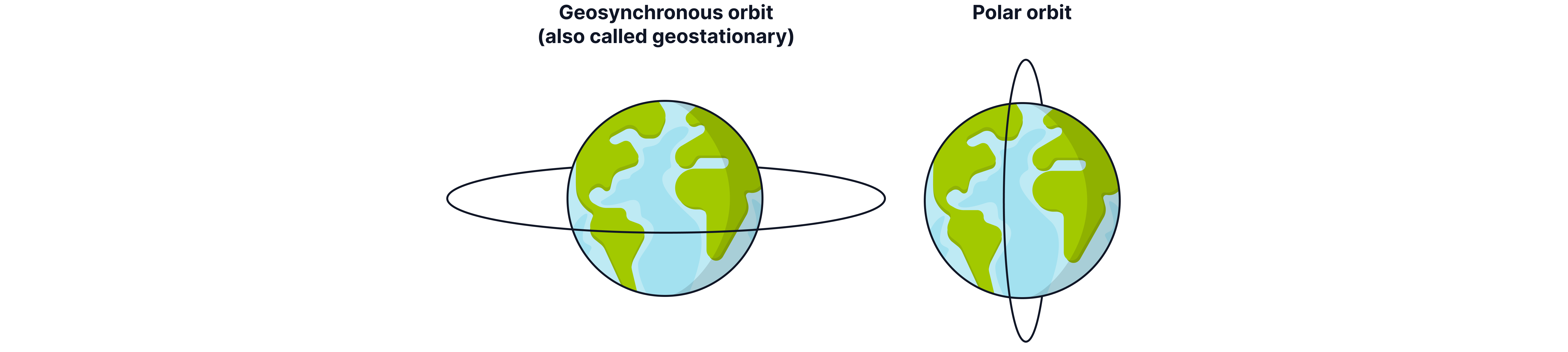
If the satellite is in geosynchronous orbit, the orbital period of the satellite is equal to the time for the Earth to rotate on its axis, . The satellite then appears to always be in the same location above the surface of the Earth. The satellite orbits in the plane of the equator and is used for things like GPS and communication networks.
Remember: The distance used in calculations is the sum of the planet's radius and the satellite's altitude. This is often forgotten in exam questions.
Worked Example
A satellite undergoes a circular orbit at a height of above the Earth’s surface. The mass of the satellite is .
Calculate the gravitational force acting on the satellite.
Calculate the orbital speed of the satellite at this radius.
Answer:
Practice Questions
A satellite, mass , is in circular motion around a point away.
Explain why the satellite is accelerating.
Each orbit takes hours. Determine the satellite’s angular speed.
Calculate the centripetal force.
-> Check out Brook's video explanation for more help.
Answer:
As the satellite orbits, the direction of its motion changes, so its velocity changes. Acceleration is the rate of change of velocity; therefore, because the satellite’s velocity is changing, it is accelerating.
Define gravitational field strength.
Describe how to measure the gravitational field
strength on the surface of the Earth.
-> Check out Brook's video explanation for more help.
Answer:
Force of gravity per unit mass.
Drop a ball bearing using an electromagnet connected to a timer. The timer is stopped when the ball hits the pad at the bottom. The height from the COM of the ball to the pad is the distance (). Repeat for different heights. Use the SUVAT equation:
Plot a graph of against , the gradient of the line can then be used to calculate gravitational field strength, .
A GPS satellite is in a circular orbit at a height , above the surface of the Earth. The Earth has mass and radius .
Show that
Calculate the orbital period of the satellite when
-> Check out Brook's video explanation for more help.
Answer: