Gravitational Potential
Brook Edgar
Teacher

Explainer Video
Gravitational Potential
Gravitational potential energy is the energy of an object due to its position in a gravitational field. It is a scalar quantity. Gravitational potential energy is defined as zero at infinity. A rocket leaving Earth needs to increase its gravitational potential energy to zero to leave Earth.
The gravitational potential, , at a point is the work done per unit mass to move a small object from infinity to that point in the field.
Rearranging the equation, , from the AQA data sheet helps you to remember this definition -> .
The gravitational potential around a body, such as Earth, is inversely proportional to the distance away from the surface, as indicated by the equation:
Formula:
Gravitational potential is negative as work is required to remove a mass from the gravitational pull of the Earth, as it is an attractive force. Energy needs to be put into the system to remove it from the Earth's surface to infinity, where the gravitational potential is defined as zero.
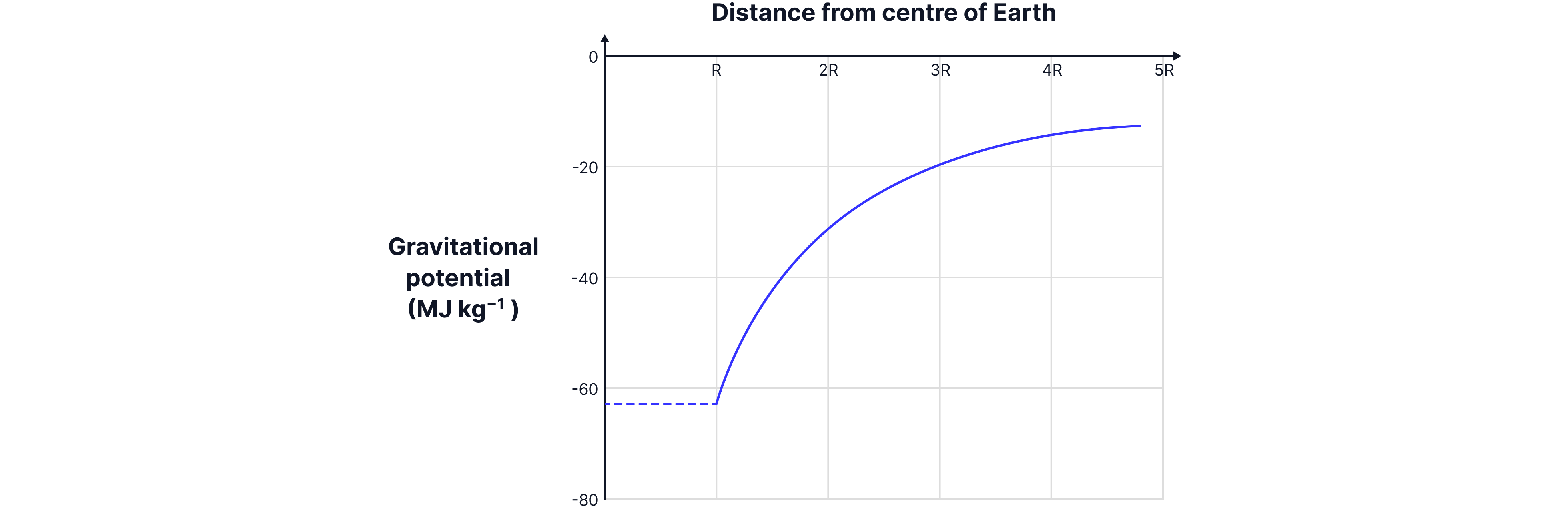
Remember: The gravitational potential lines around a spherical object are negative, as infinitely far away from the object is defined as zero, and work must be done on a unit mass against gravity to move the unit mass from a point near the object to outside the field.
Worked Example
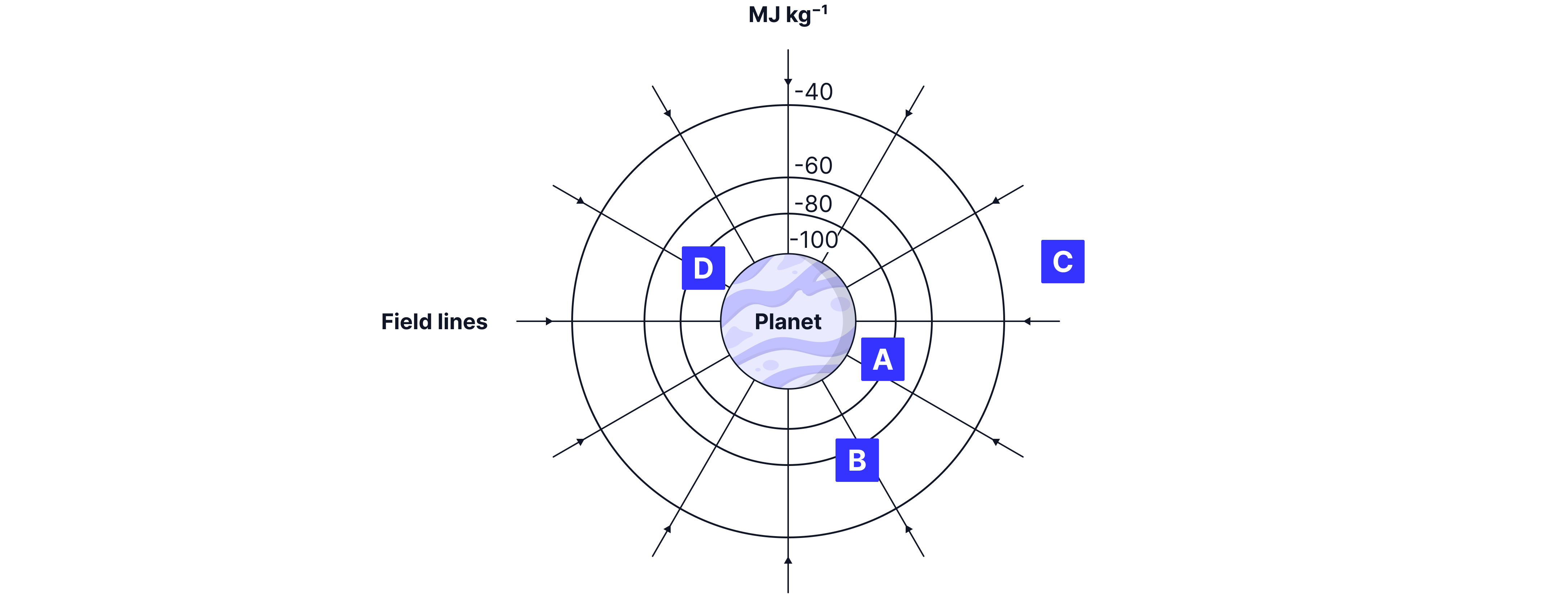
For the diagram above, state the energy needed to move a mass between the following points:
From A to B
From A to C
From infinity to A
From A to D
Answer:
This is the opposite of question two. It is the same magnitude of energy but negative, . Bringing the mass into the field, no work is required, as gravity is an attractive force, so the negative tells us that energy is released from the system.
A and D are on the same gravitational potential lines, . They are on equipotential lines. No work is required to move between them,
Teacher Tips: Care to read the units on the axis og graphs given, as the potential lines here are measured in , so in moving from A to B the change in potential is .
Worked Example
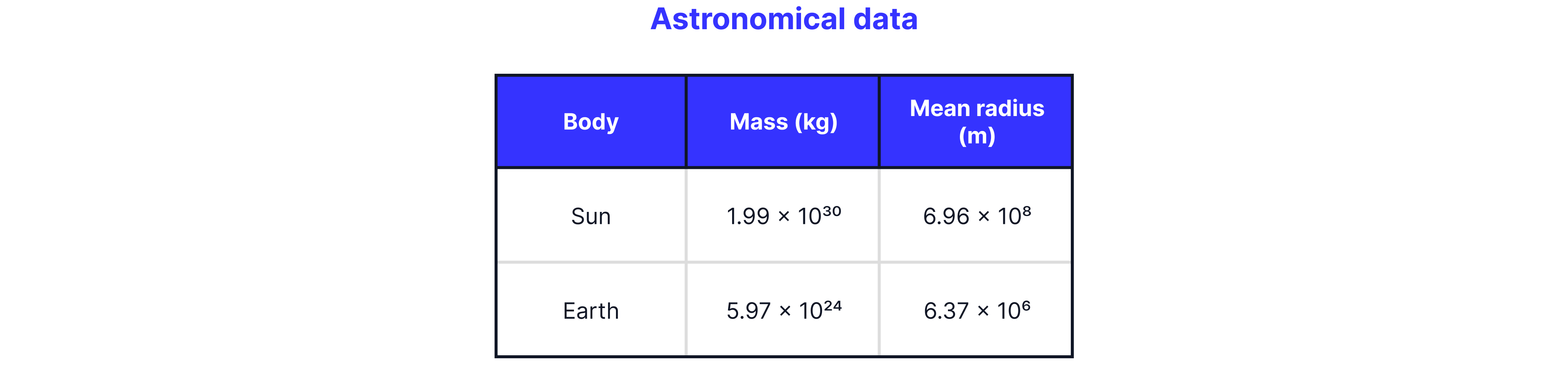
Using the table below:
Calculate the gravitational potential on the surface of the Earth.
State why the answer to question one is negative.
Calculate the energy required to send a 3.0 kg mass from the surface of the Earth to infinity.
Answer:
Gravity is an attractive force. Therefore, to remove something from the Earth's surface, you have to put in work. As the gravitational potential at infinity is zero, the potential lines around the Earth must be negative.
Teacher Tips: In question three the change in potential is to move from the potential line of . This change is then an increase of .
Orbiting Satellites
Some problems can ask you to calculate the change in energy required to move between two altitudes above the surface of a planet. There are two steps involved here. Firstly, we need to calculate the gravitational potential at each point and then calculate the change in energy required to move between these two potential lines.
For example, to calculate the energy required to send a satellite, mass , from above the surface of the Earth to , we know from the equation, , which will become that we first need to calculate the change in gravitational potential.
->
Remember: When calculating, , the distance we need to include the radius of the object, for example, when at an altitude of km above the Earth's surface, we need to include the radius of the Earth so the total distance is km.
An orbiting satellite has both kinetic energy due to its orbital speed and potential energy due to its height above the surface of the planet.
As the satellite moves away from the surface of the planet, its kinetic energy decreases and its gravitational potential energy increases, as shown below:

To calculate the gravitational potential energy, we combine the two equations below:
->
The total energy of the orbiting satellite can now be stated as:
Orbital velocity can be rewritten in terms of mass of the planet and orbital radius by combining the equations of centripetal force and gravitational force of attraction between the two bodies, as we have done before:
The total energy of the orbiting satellite can now be stated as:
Practice Questions
The diagram below shows the equipotential lines for a uniform gravitational field. The lines are separated by .
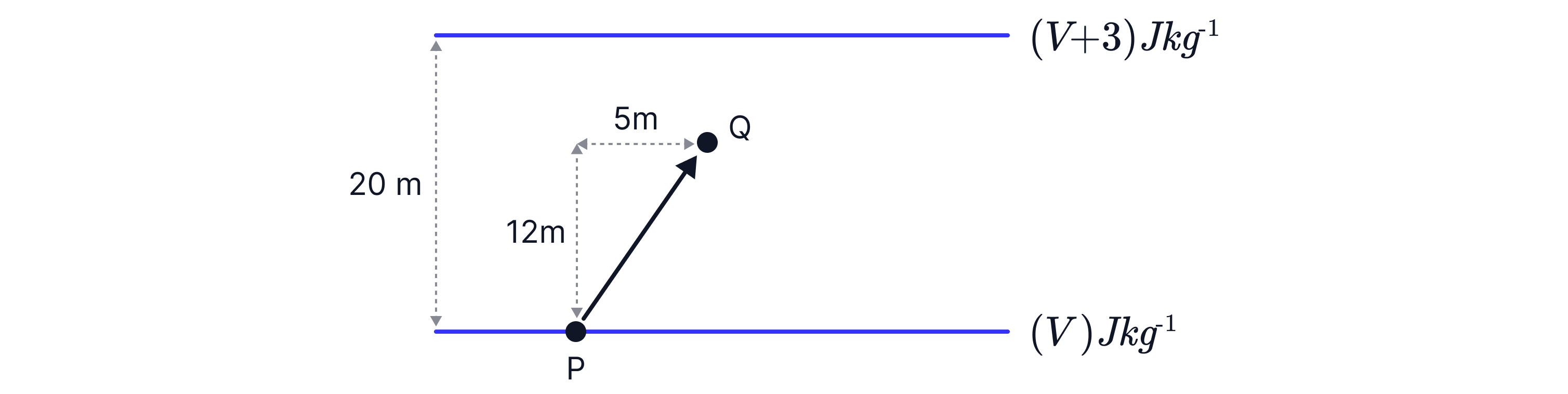
An object of mass is moved from P to Q. Calculate the work done against gravity to move the object.
-> Check out Brook's video explanation for more help.
Answer:
A satellite of mass is in a geostationary orbit with an orbital radius of .
Define geostationary orbit.
Calculate the gain in gravitational potential energy as the satellite is placed into orbit.
-> Check out Brook's video explanation for more help.
Answer:
Period of orbit is hours. Orbit is in the equatorial plane. Satellite remains in a fixed position relative to the Earth.
Complete the table for gravitational potential at a distance r from the centre of the Earth.
-> Check out Brook's video explanation for more help and for the rest of that year's exam question.
Answer: