Moments
Brook Edgar
Teacher

Explainer Video
Moments
A moment is the turning effect of a force about a point.
Formula:
To calculate the size of the moment caused by the force below:
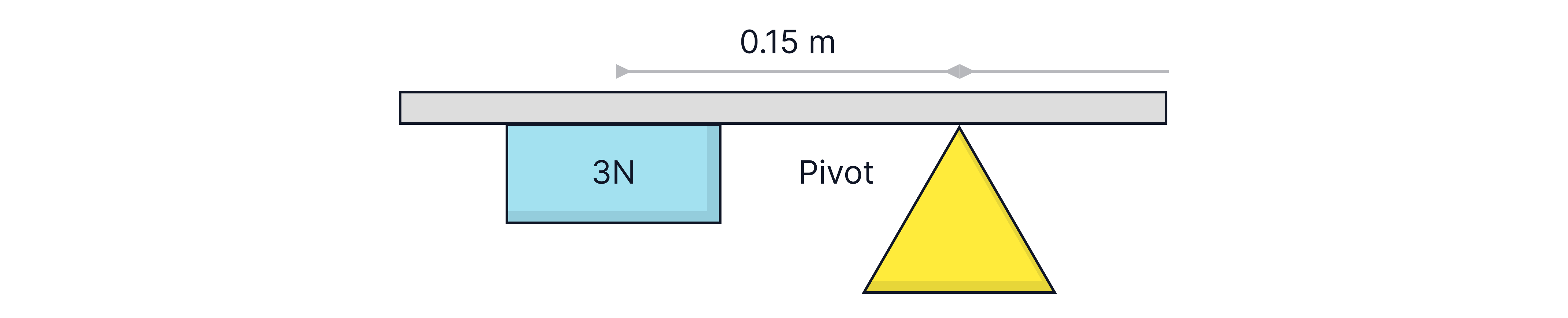
The moment is in the anticlockwise direction about the pivot.
The moment of a force about any point is the product of the force and the perpendicular distance from the point to the line of action of the force. Sometimes we are given forces at angles, so we need to remember how to resolve forces.
For example, to find the moment acting about point A on the bar below, we first need to resolve the force into its parallel and perpendicular components to the bar.
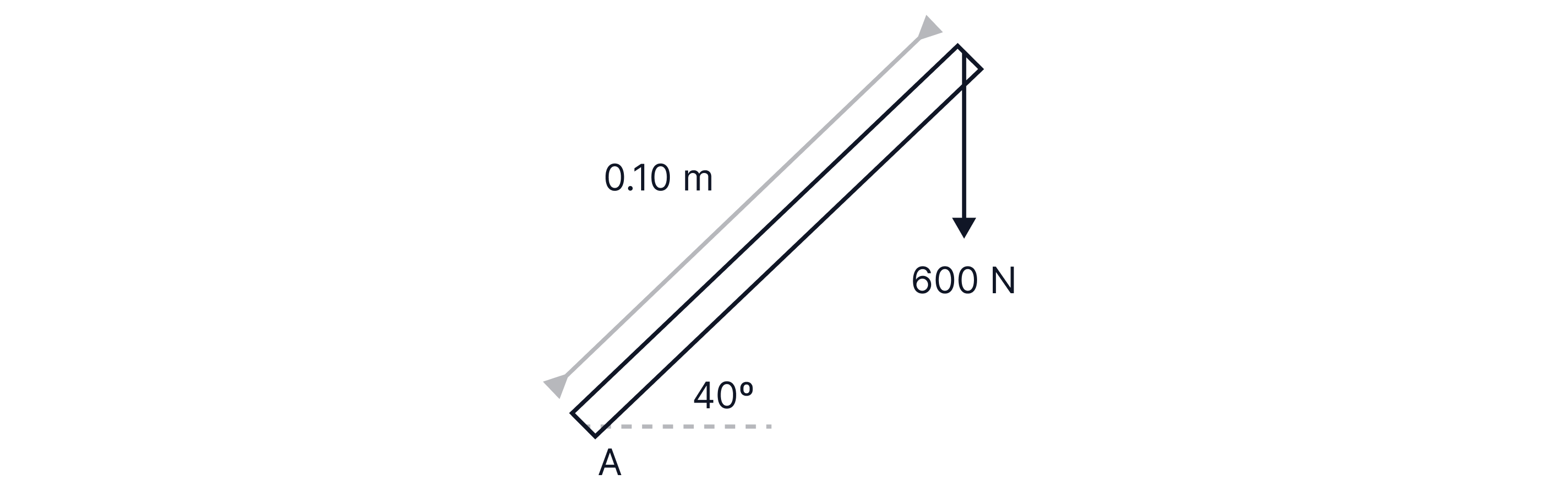
The perpendicular component of the force to the bar that we are interested is highlighted by the green arrow below:
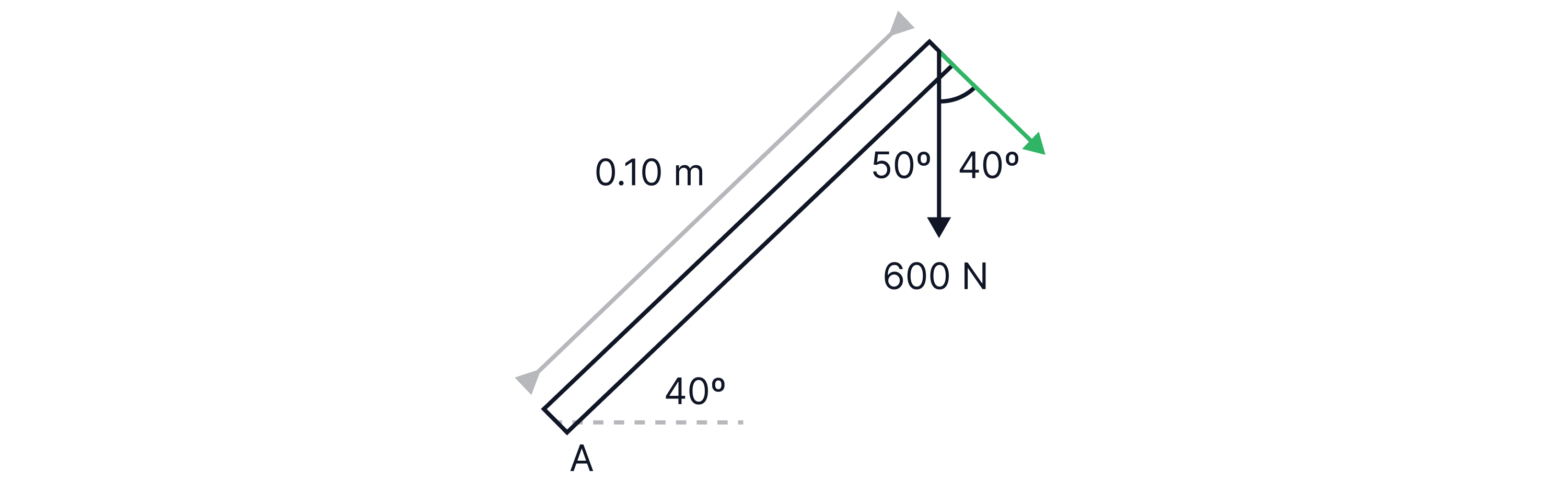
The magnitude of this component is . To calculate the moment of this force about point A:
Worked Example
Calculate the moment acting around point B on the bar below:
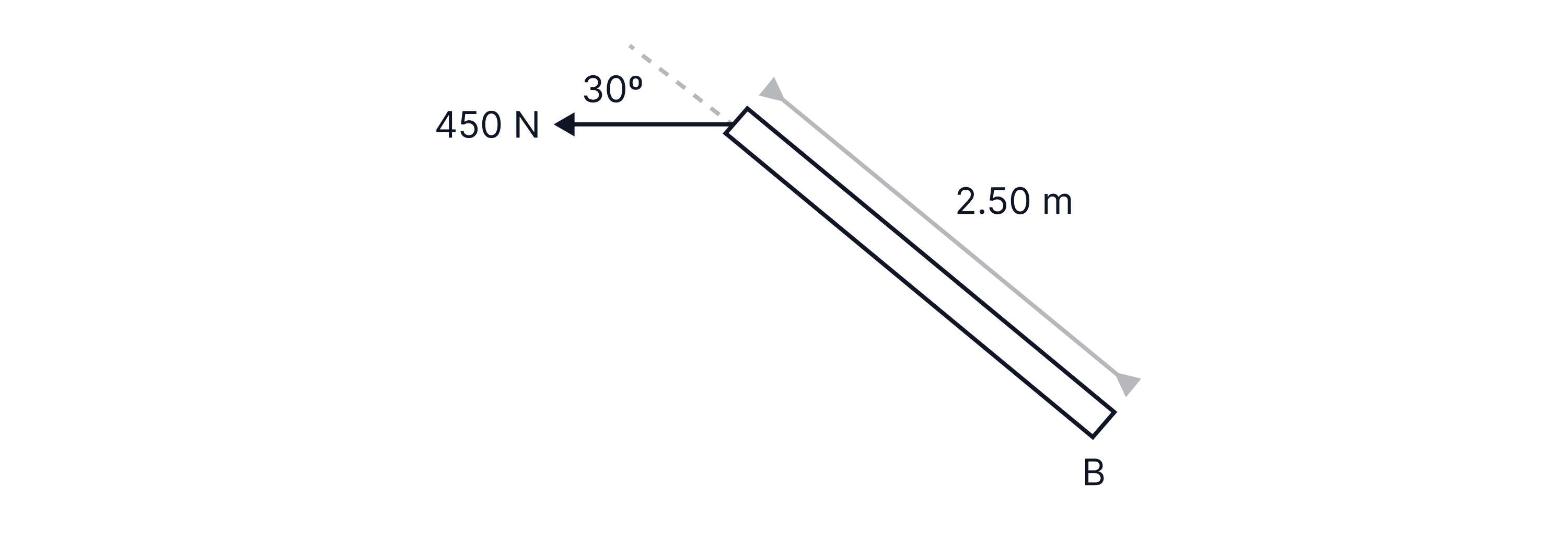
Answer:
Resolve the force into its parallel and perpendicular components to the bar:
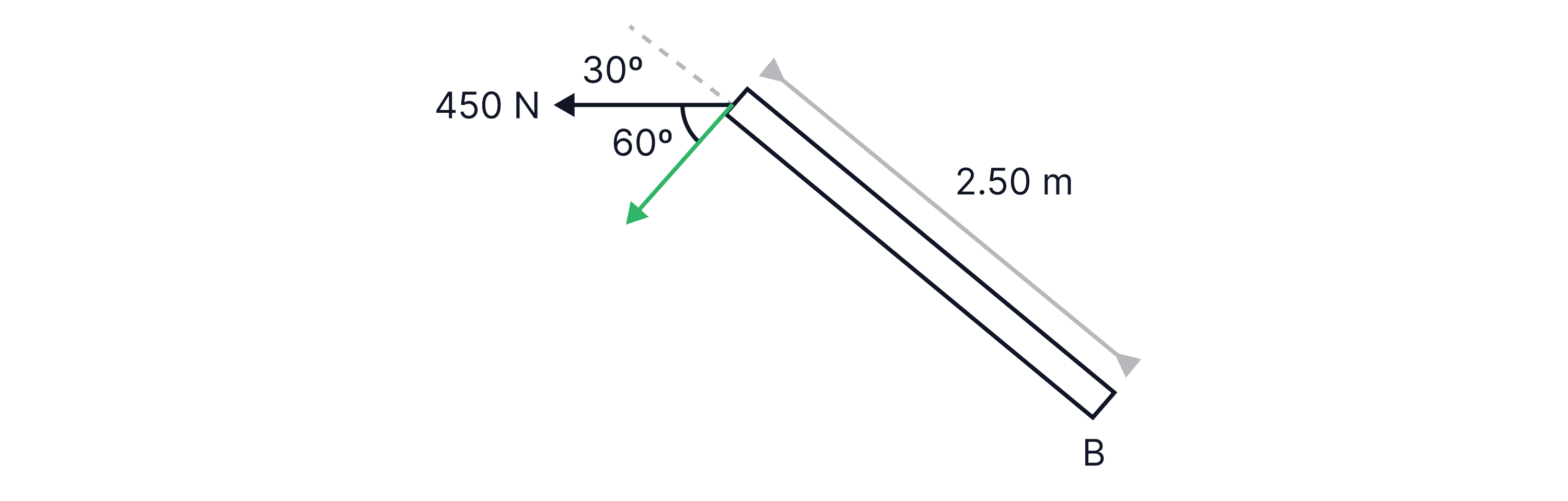
The perpendicular component of the force to the bar is .
Worked Example
Calculate the size of the clockwise moment on the wrench.
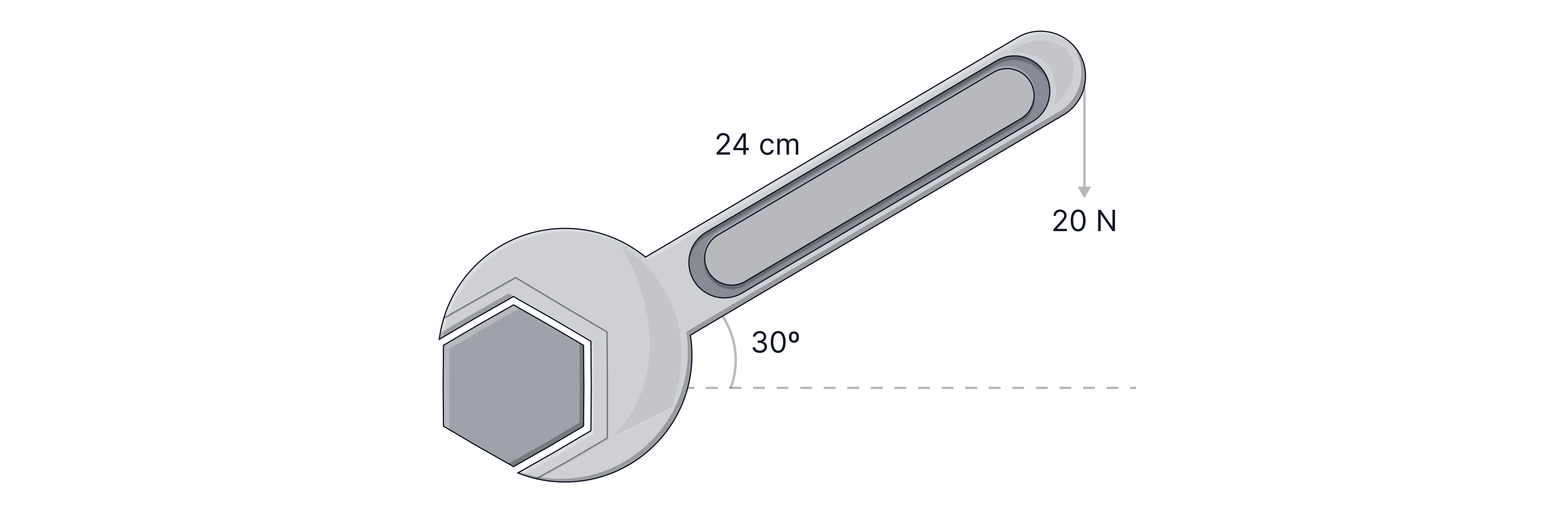
Answer:
Teacher Tips: This time, it was easier to resolve to find the component of the distance that is perpendicular to the line of action of the force. The force is directly downwards, so we need to find the horizontal component of the distance. In questions you can resolve either the distance or the force, whichever you see as easier.
Equilibrium
Two conditions must be satisfied for an object to be in equilibrium:
Linear equilibrium: The vector sum of forces is zero (the resultant force equals zero).
Rotational equilibrium: The sum of clockwise moments equals the sum of anticlockwise moments about any point.
We can apply the conditions above to solve for the weight of the beam below and to calculate the force at the pivot.

We are going to start by taking moments about the pivot, as we can then ignore any forces that act there.
The anticlockwise moment caused by the force must balance the clockwise moment from the beam's weight.
To calculate the force at the pivot, we could take moments about the point where the weight acts, or we could use linear equilibrium, knowing that all the upward forces must balance the downward forces.
Here, we were told the distance from the pivot at which the weight of the beam acts; however, sometimes in questions, we are told that the weight of the beam/shelf is uniform. This means that the weight of the beam is considered to act at its midpoint. Other times, we are told that the mass of the beam/shelf is negligible; in this case, we ignore it from our calculations.
Worked Example
The diagram shows a horizontal rod attached to the wall by a hinge and held in place by a string. The rod has negligible mass.
Calculate the tension in the string.
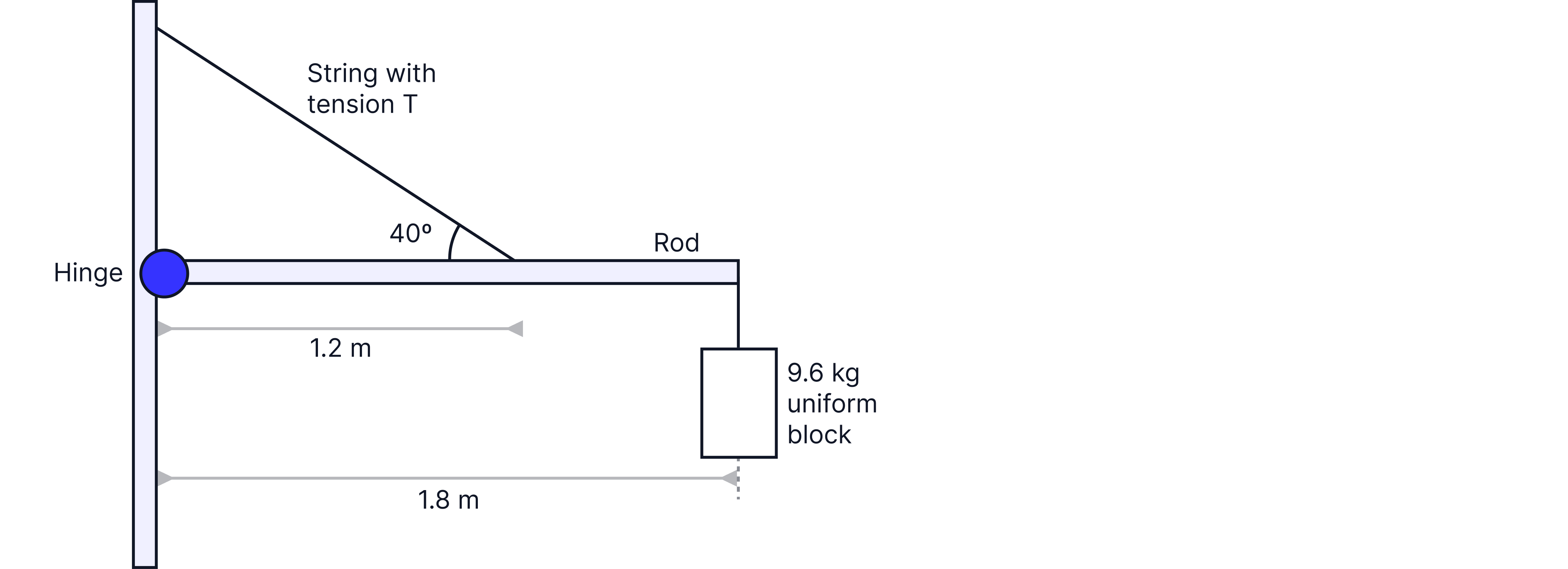
Answer:
As we want to calculate the tension, we will take moments about the hinge, as we are not given information about any forces acting there, so we want to ignore them.
The clockwise moment of the block about the hinge:
The clockwise moment of the block about the hinge = the anticlockwise moment of the tension in the string about the hinge. The vertical component of tension is perpendicular the rod so produces the anticlockwise moment.
Teacher Tips: ALWAYS take moments about the point where you want to ignore the forces acting there. As the distance to the pivot is zero, the moment is also zero and can thus be ignored.
Practice Questions
Calculate the force at the pivot.
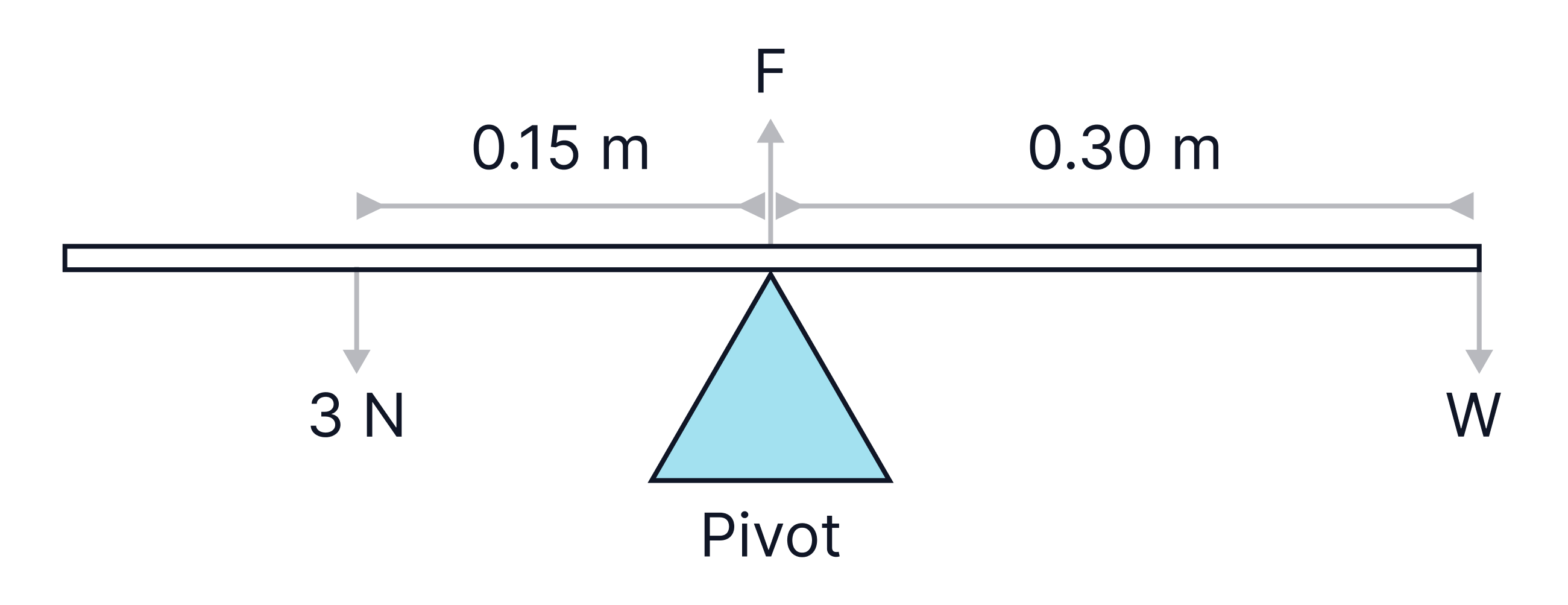
-> Check out Brook's video explanation for more help.
Answer:
A uniform diving board, long with a mass of , is attached at A and rests on a fixed support at B. The diver’s mass is .
Find the force at A and B.

-> Check out Brook's video explanation for more help.
Answer:
Force at A = down
Force at B = up