Impulse
Brook Edgar
Teacher

Explainer Video
Momentum
Momentum is a property of moving objects that is directly related to the object's mass and velocity.
Formula:
Velocity is a vector, which means that the direction of motion is important. Momentum is also a vector quantity.
The law of conservation of momentum states that momentum must be conserved in a system if there are no external forces acting on it. This means that the total momentum of a system before an event must be equal to the total momentum after the event.
For example, if a moving ball collides with another, causing them to stick together and move off together, as shown below, we can calculate the velocity they move off at as long as the initial velocities and masses of the objects are known.

We know that total momentum is conserved, taking the direction to the right to be the positive direction, we can calculate the momentum of both balls before the collision.
The total momentum after the collision must also be . As the two balls are stuck together and move off together as one object, the mass is now their combined mass.
Worked Example:
A rifle fires a bullet at a velocity of . The bullet has a mass of .
Calculate the velocity of the rifle after it has been fired.
Hint: What is the total momentum of the gun before it is fired?
Answer:
The momentum before the gun fires is zero, as the gun is stationary, and thus the bullet inside the gun is also stationary.
The total momentum after the gun fires must also be zero. The bullet has a positive velocity, so we will take the right to be positive; therefore, anything moving to the left will have a negative velocity.
We have just shown that the rifle moves in the opposite direction to the bullet, backwards at a much slower speed. This is known as recoil.
Total momentum and total energy are always conserved in closed systems. Kinetic energy is conserved in elastic collisions. If kinetic energy is not conserved, it is an inelastic collision.
Worked Example
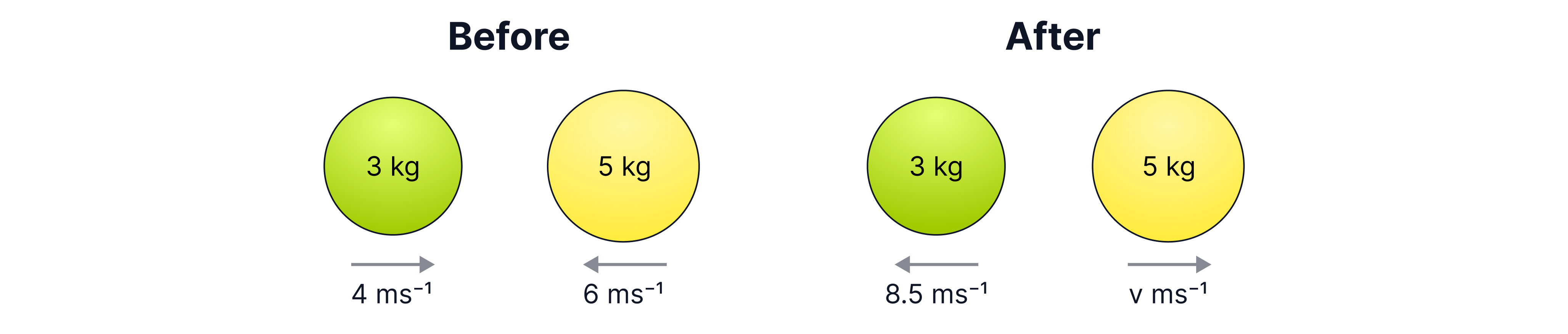
Two particles moving in opposite directions collide and rebound as illustrated below. Calculate the missing velocity of the ball after the collision. Deduce if the collision is elastic or not.
Answer:
Before, the balls are moving in different directions, and as velocity is a vector, we are going to define to the right as positive. Therefore as the ball is moving to the left its velocity is negative.
The total momentum after the collision must also be .
To determine if the collision is elastic or inelastic, we need to see if kinetic energy is conserved by calculating the total kinetic energy before the collision and seeing if it equals the total kinetic energy after the collision.
Kinetic energy before the collision:
After:
Kinetic energy is conserved, so the collision is elastic.
Impulse
Resultant force is directly proportional to the rate of change of momentum.
Change in momentum is also referred to as impulse.
Formula:
Increasing the time taken for the same change in momentum lowers the impact force. This is why you should bend your knees when you jump and land, as the time taken for your knees to bend on landing increases the time taken for the same change in momentum, reducing the impact force on your body. Similarly, you are less likely to hurt yourself when falling onto a crash mat rather than the ground, as the time taken for the mat to compress increases the time taken for the same change in momentum, reducing the force.
Worked Example
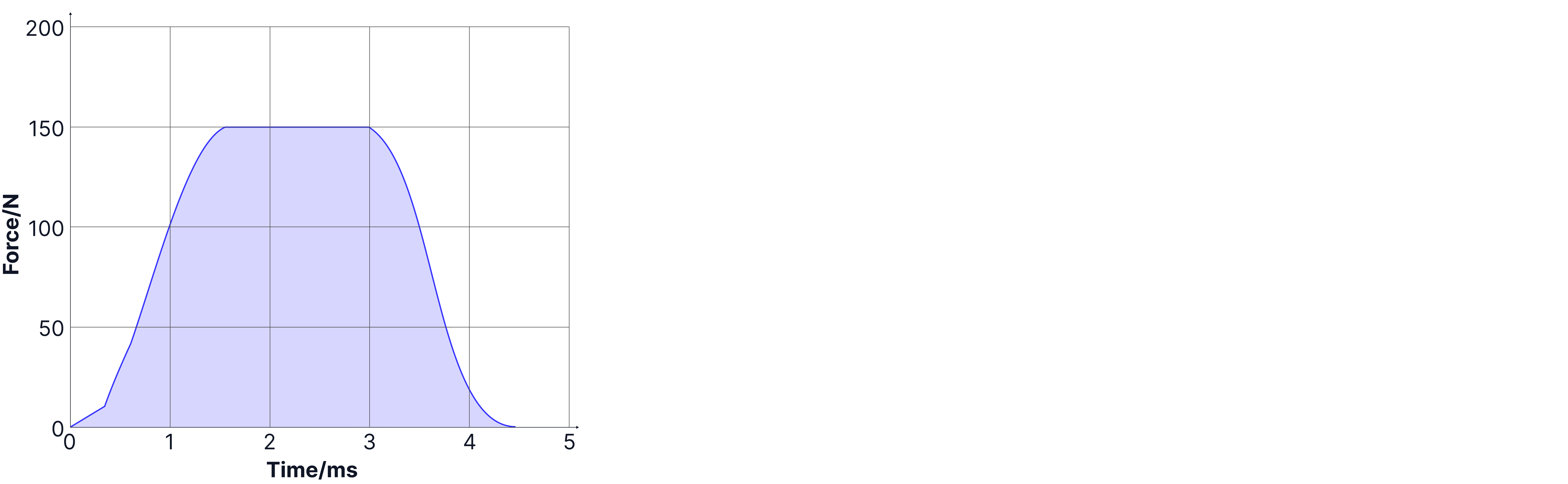
The graphs below show how the force on a ball changes with time. The ball was initially stationary. Calculate the final velocity of the ball in each case.

Answer:
The area under the graph = Impulse, the change in momentum. As the initial momentum of the ball is zero, as it was stationary, the area under the graph will tell us the final momentum of the ball and thus its velocity, as we know the ball's mass.
For graph one we can calculate the area under the graph is that of a triangle:
For the second graph, we can not easily find the exact area under the graph. A tip is that in exams, if they give you a graph like this with very large squares, they want you to count the squares. The total area is then the area of one square times by the total number of squares under the graph.
Number of squares:
Area of square:
Total area under the graph:
Teacher Tips: Don't forget to check the units on the axis; many forget to see that in the second graph, time is in milliseconds.
Worked Example
Explain how the items in the delivery box are protected.

Answer:
The change in momentum for a falling box with or without bubble wrap is the same (i.e. they both hit the ground at the same speed and stop).
However, bubble wrap increases the time taken for the same change in momentum to occur as it takes time for the bubble wrap to compress/deform upon impact. As force equals the rate of change of momentum, an increase in time results in a smaller impact force and thus the items inside the box with bubble wrap are less likely to break.
Worked Example
In a safety test a truck moving at hits a wall. The front of the truck crumples by as the truck is brought to rest. Calculate the average force on the truck during impact.
Answer:
First, we need to calculate the time taken for the deceleration to occur. This can be done using SUVATs if we assume that the deceleration is constant.
We can now calculate the force knowing that force is equal to the rate of change of momentum:
Practice Question
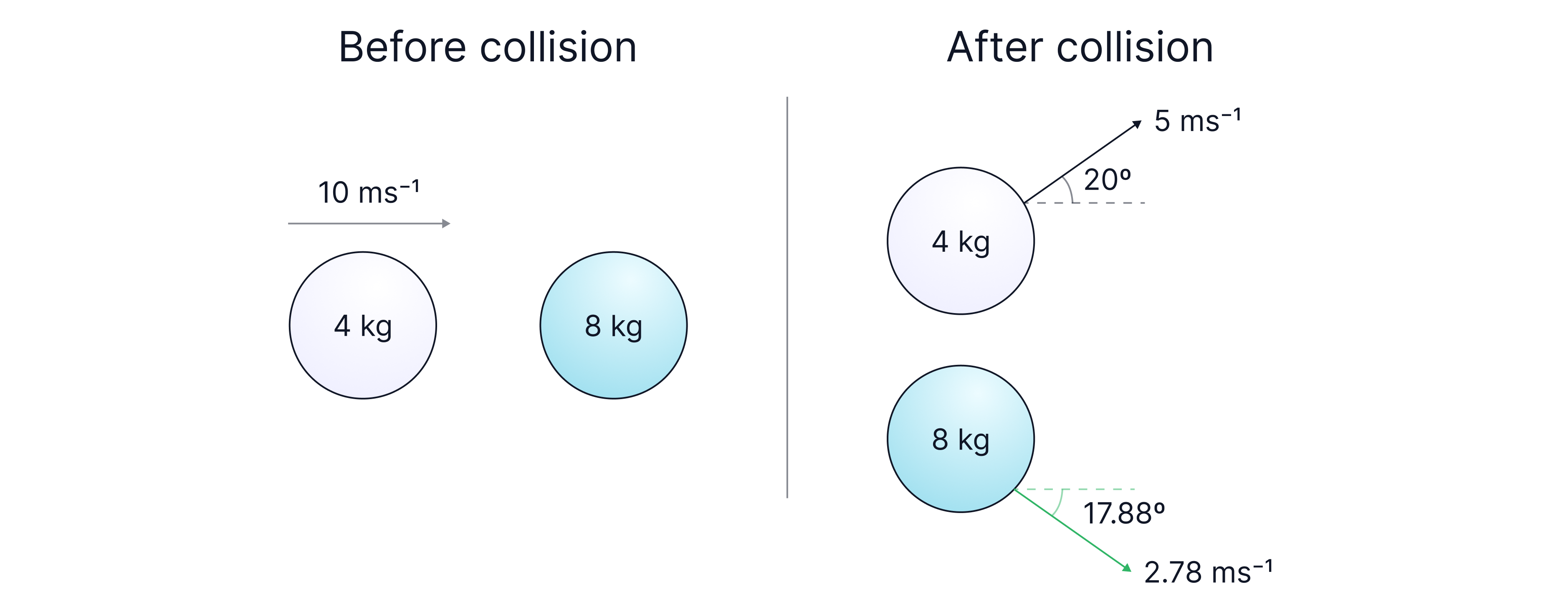
Calculate the speed and direction of the ball after the collision shown in the diagram below.
Hint: Momentum in the vertical and horizontal directions must be conserved.

-> Check out Brook's video explanation for more help.
Answer: