Motion along a straight line
Brook Edgar
Teacher

Explainer Video
Distance-time Graphs
Graphs are used to represent information quickly. It is important that you read graphs carefully, checking the units on the axes and the number that the scale begins at - they do not always start at zero!
Here is an example situation that can be represented on a graph easily.
I leave school on foot and walk towards the shops, covering the first 6 metres in 12 seconds. I then saw my friend and stopped to chat; we only talked for 8 seconds. The shop is closing soon, so I ran the remaining 24 metres to the shop in 10 seconds.
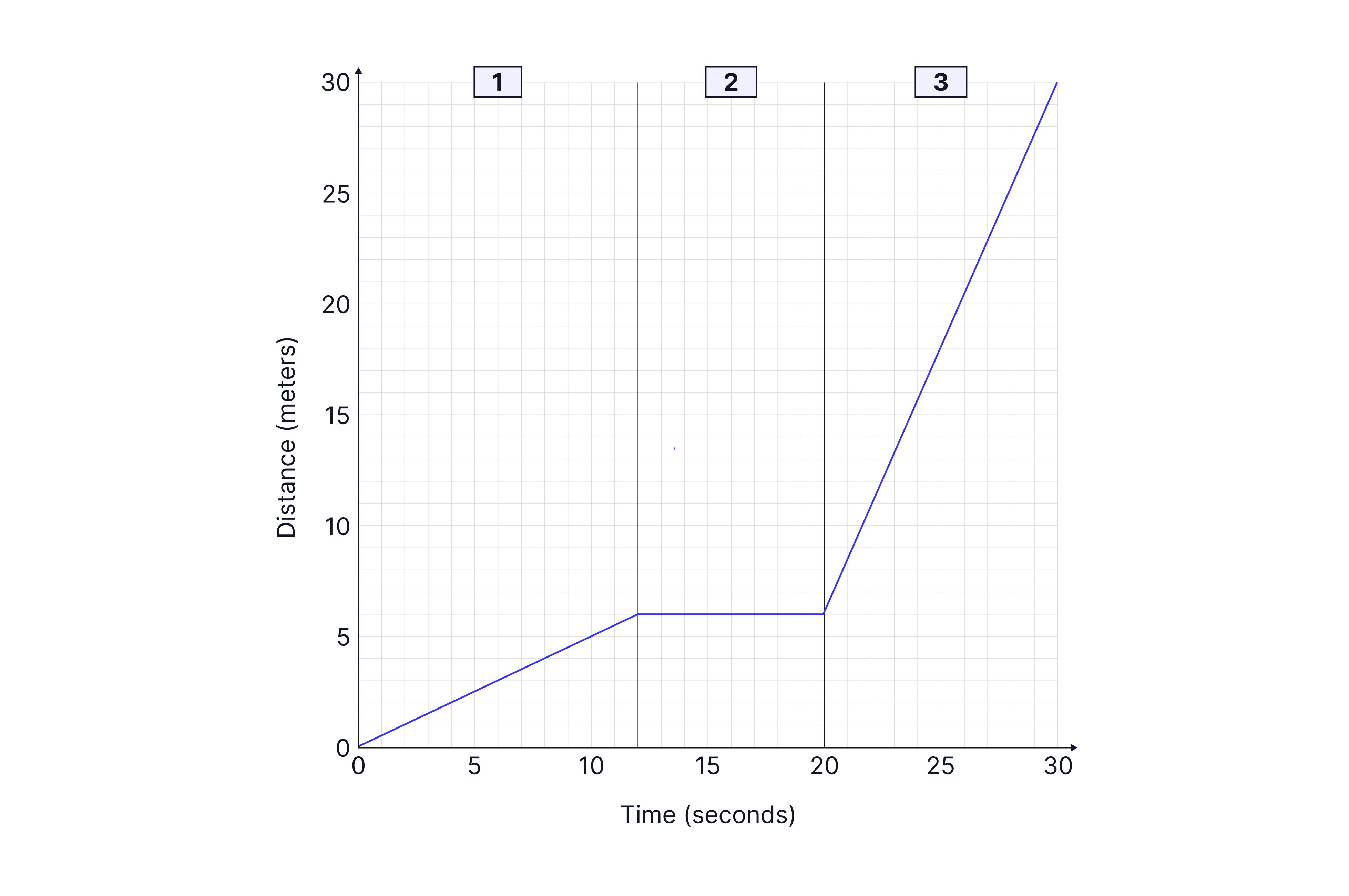
By looking at the graph, we can see when I am walking, standing still (flat line) or running (steeper line) quickly, but we can also calculate the gradient to find exact values:
Formula:
Gradient
Part 1 -> gradient =
Part 3 -> gradient =
The gradient of a distance–time graph tells us the speed.
If it were a displacement-time graph, the gradient would determine the velocity:
If the gradient is increasing; the velocity is increasing -> accelerating.
If the gradient is decreasing; the velocity is decreasing -> decelerating.
Worked Example
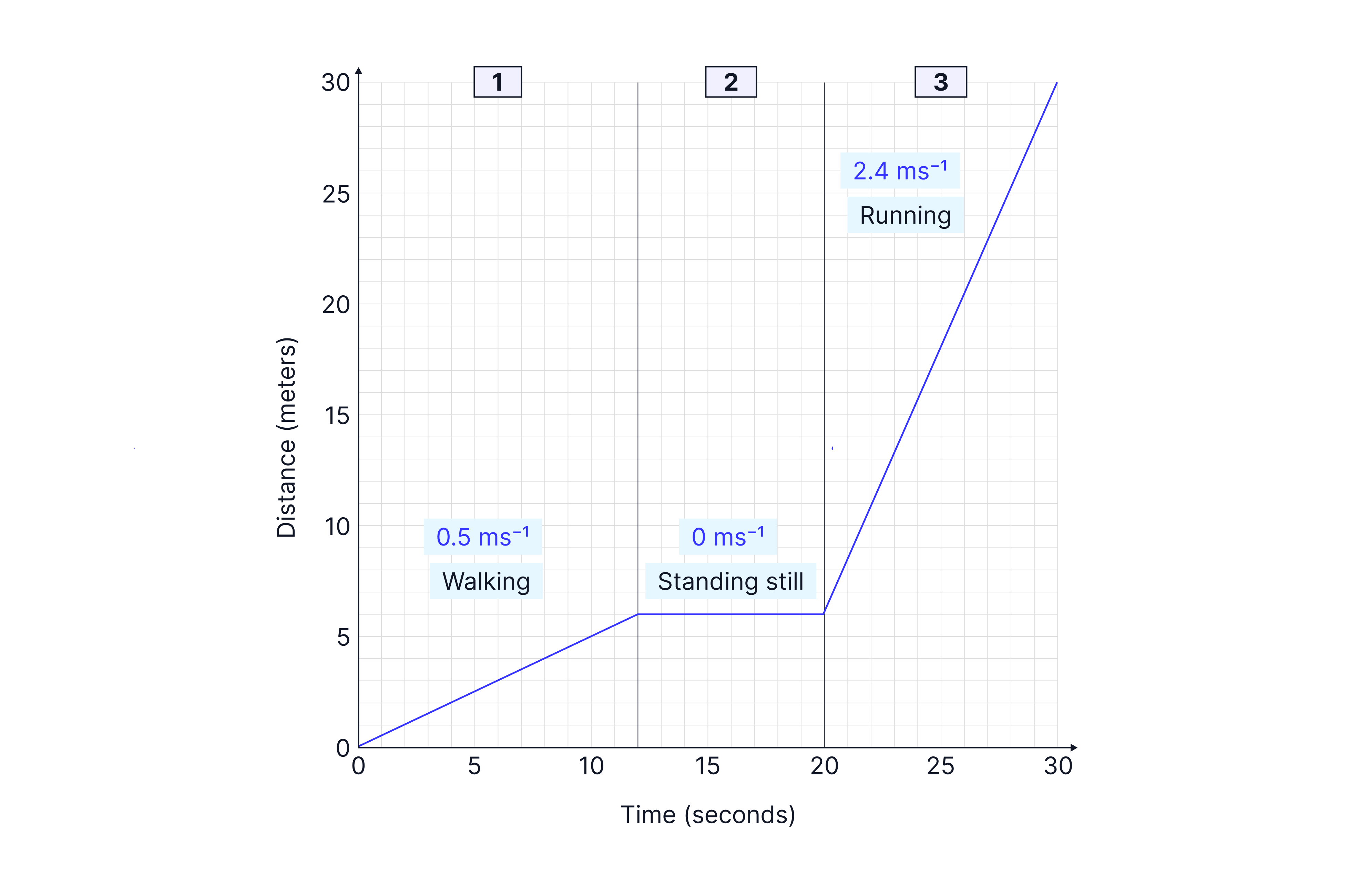
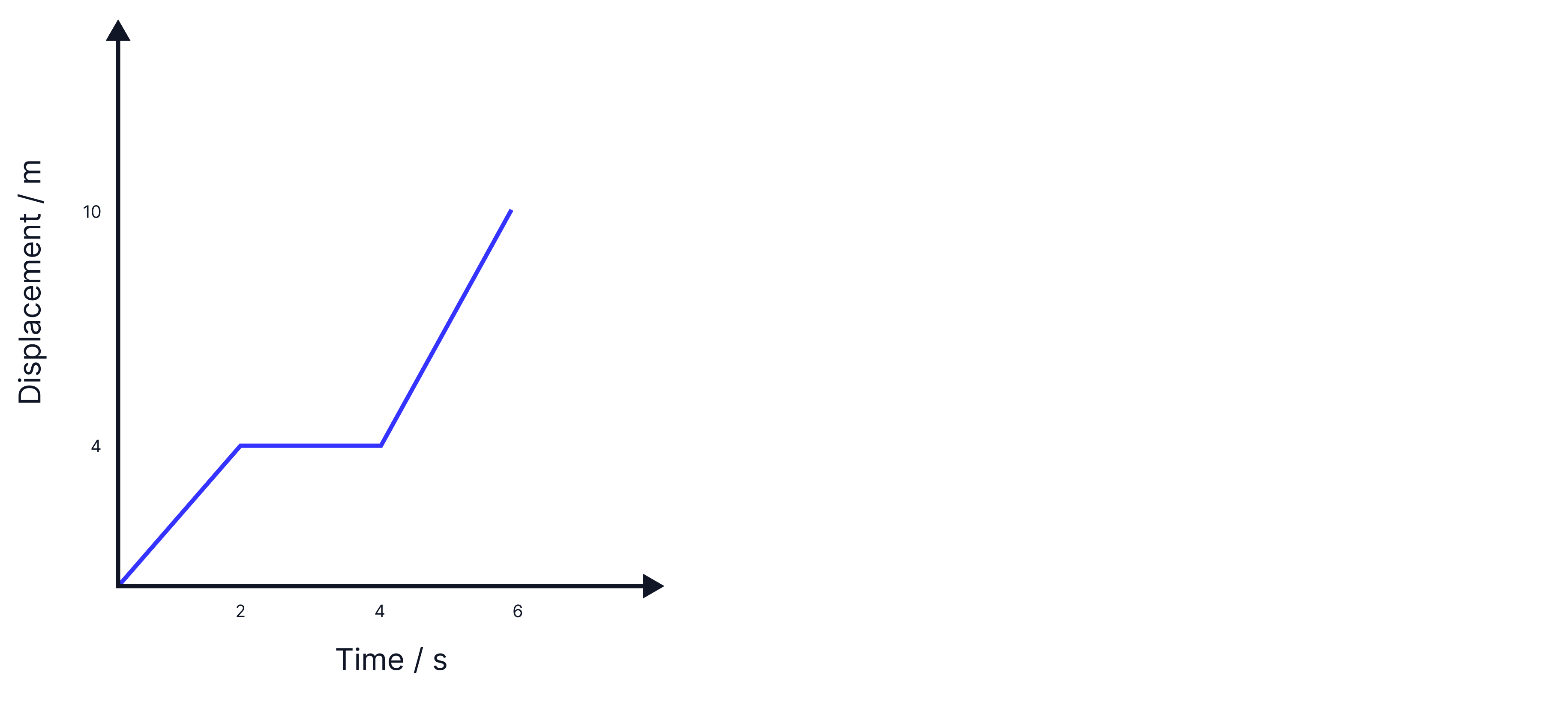
Describe the object's motion at each stage, and calculate the velocity at each stage.
Answer:
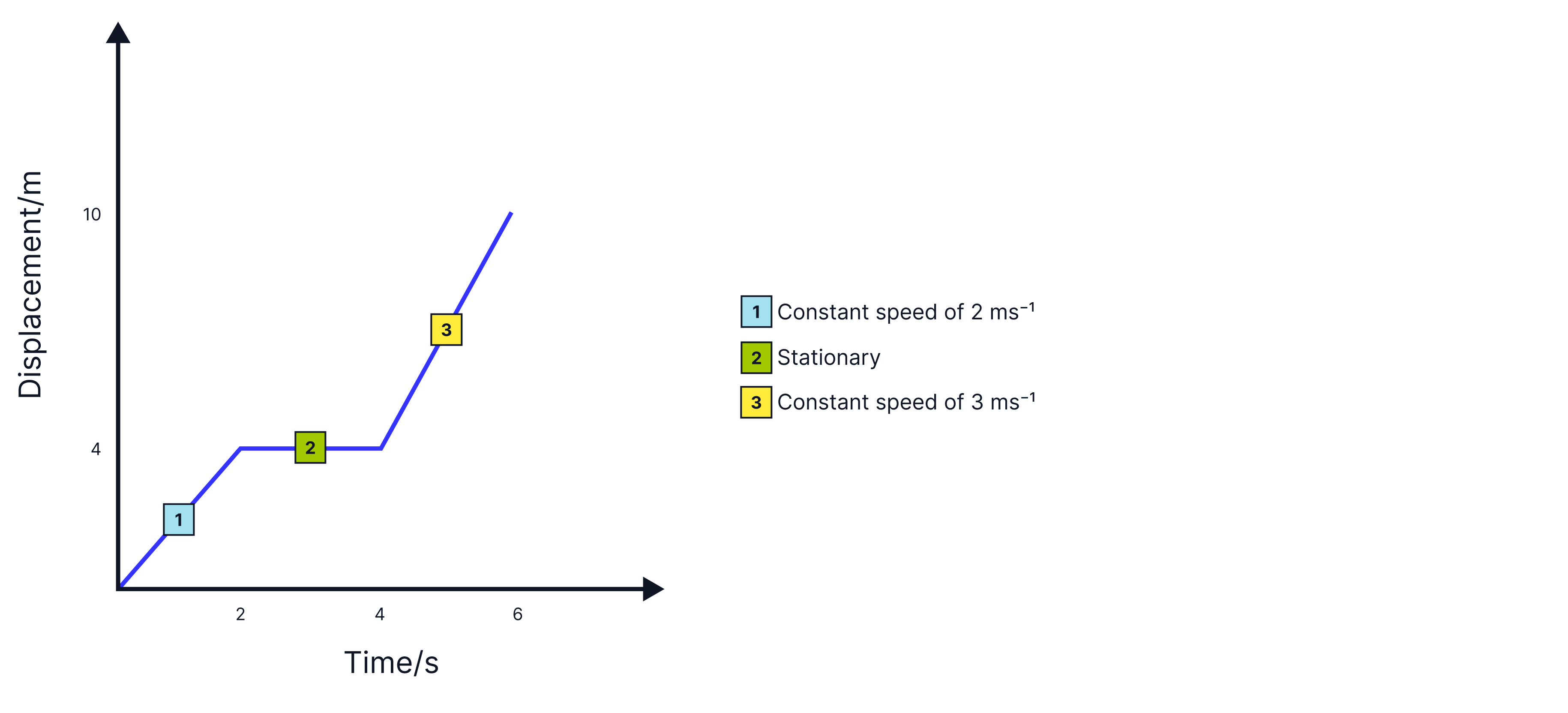
We can separate the graph into three different sections of motion:
Constant speed of,
Stationary
Constant speed of,
Worked Example
Describe the object's motion at each stage, and calculate the velocity at each stage.
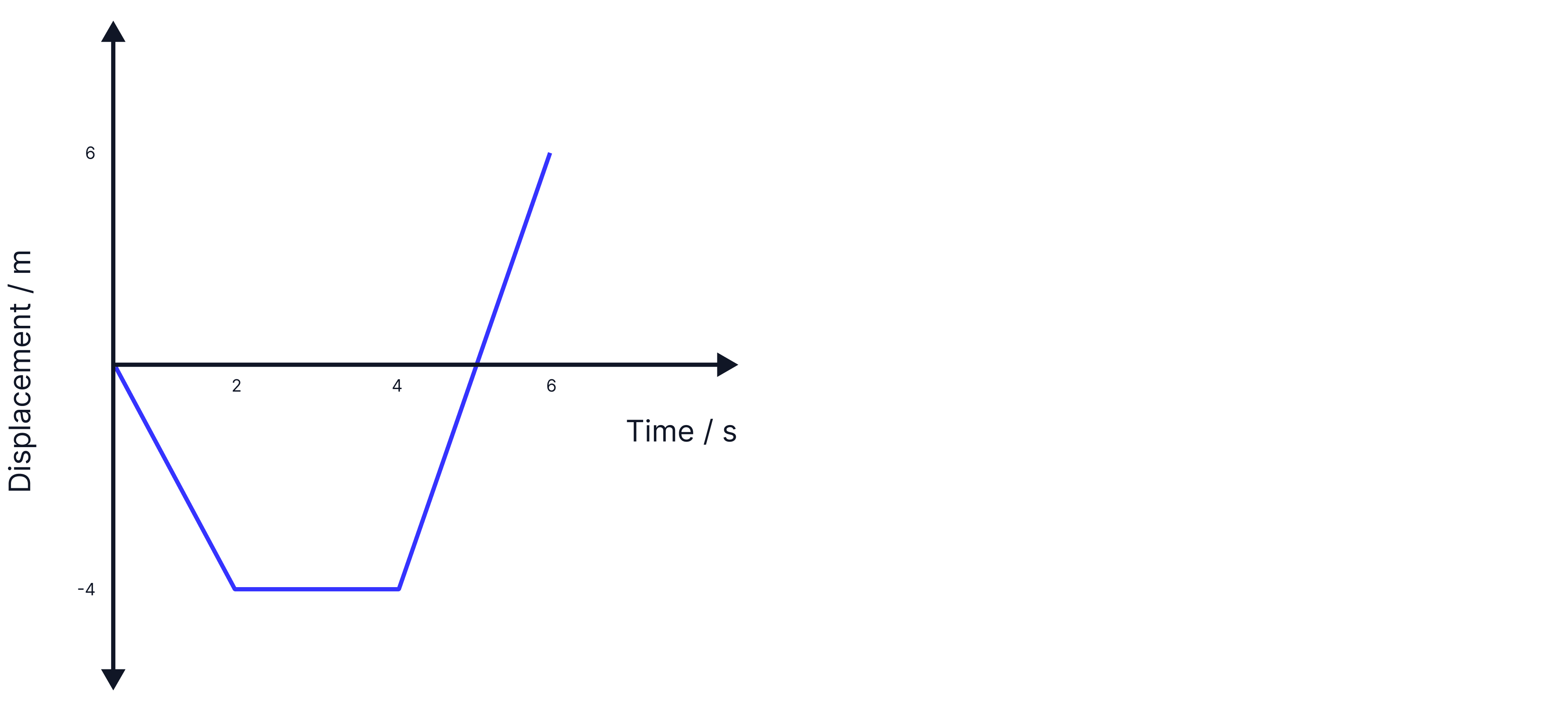
Answer:
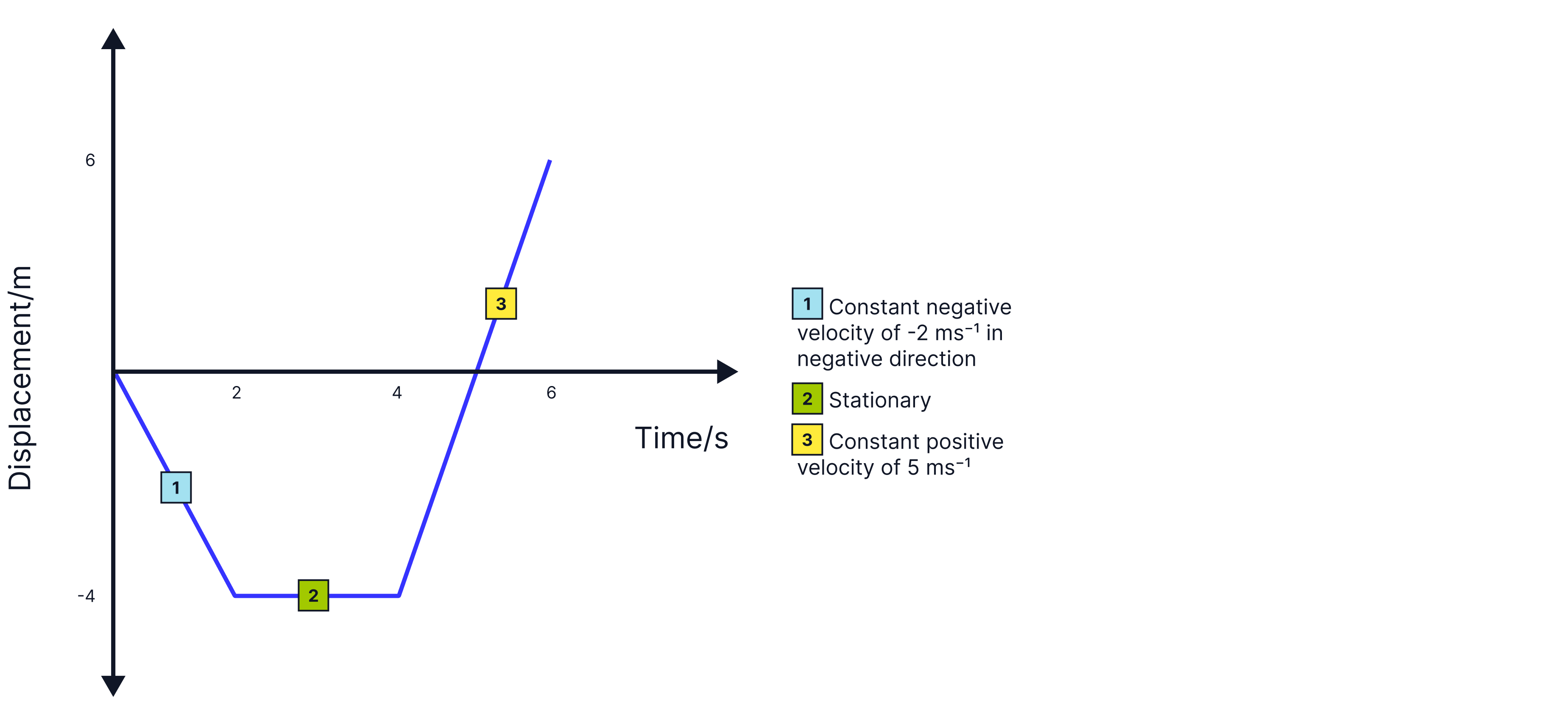
We can separate the graph into three different sections of motion:
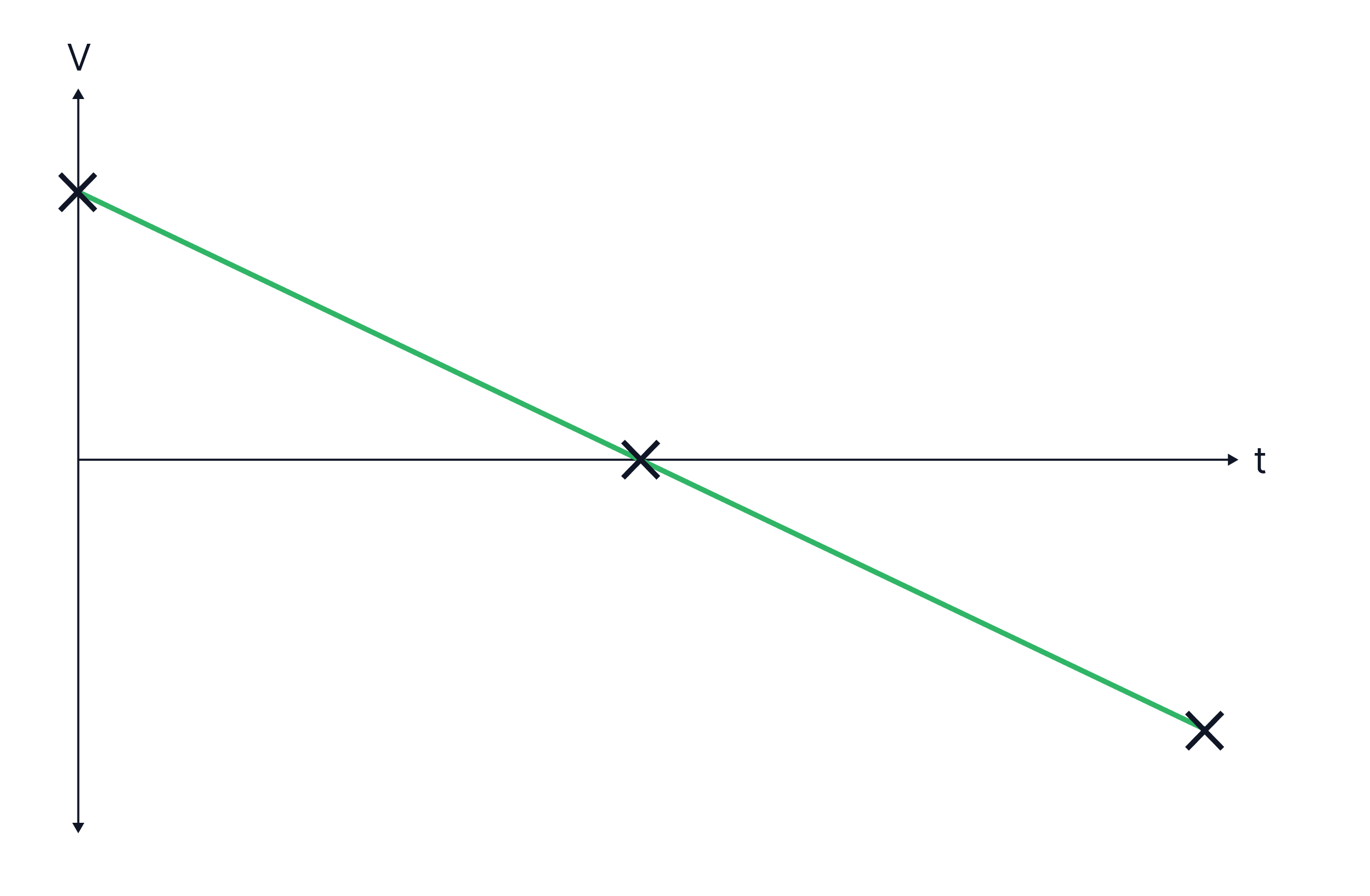
Constant negative velocity of, , which tells us that the object is moving at in the negative direction / to the left.
Stationary
Constant positive velocity of, , which tells us the object has changed direction and is now moving in the positive direction / to the right.
Teacher Tips: Remember that velocity is a vector; the negative does not mean a very small number, as the lowest speed is zero, so the negative implies direction, up/down or left/right.
If the line is curved, to calculate the gradient at a specific point, you draw a tangent to the curve and calculate the gradient of that tangent.
For example, to calculate the instantaneous velocity at we begin by drawing a tangent to the curve at that point:
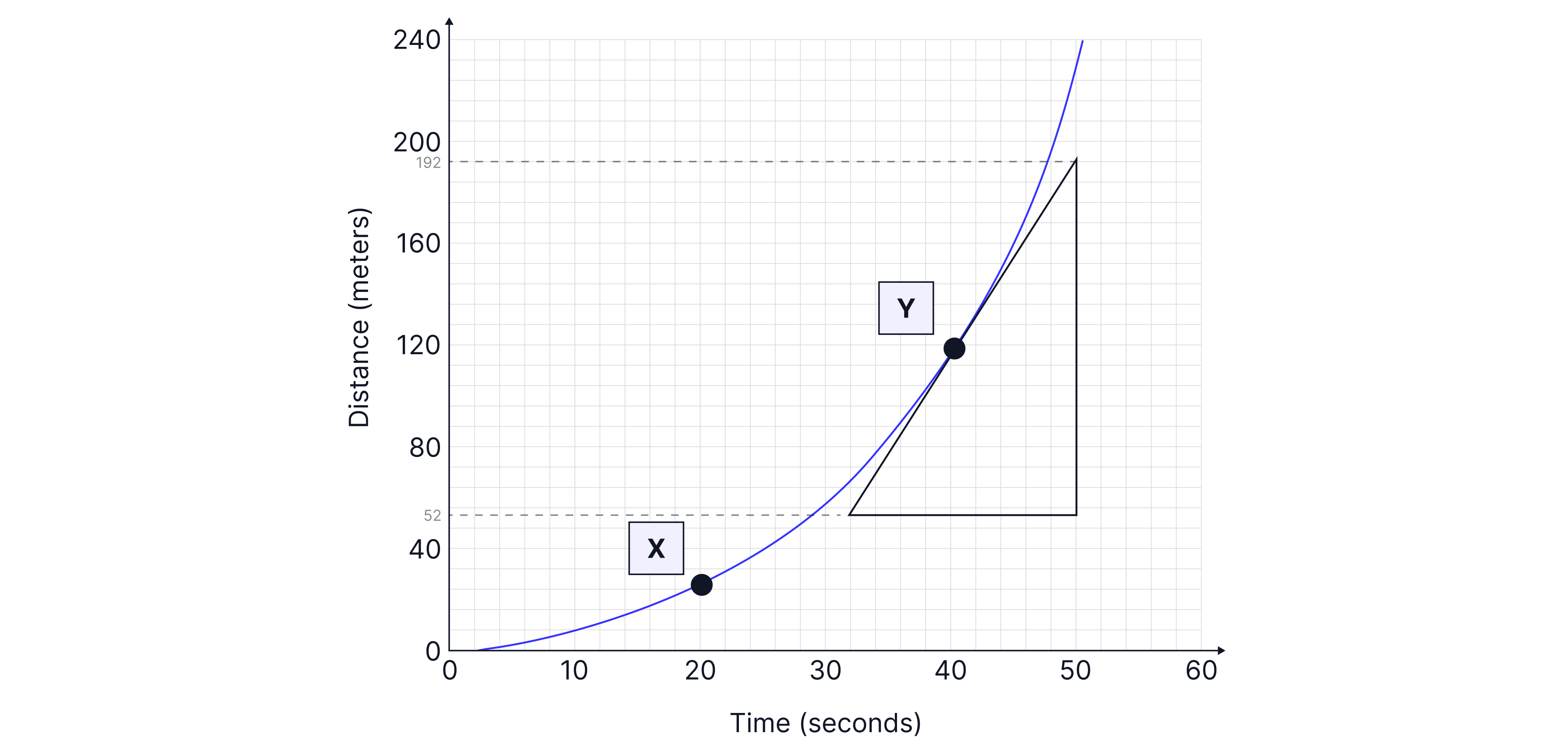
To calculate the gradient of our tangent, we want to draw a large triangle, with one side bigger than if possible.
If we were asked to calculate the average velocity, we would calculate the total displacement divided by the total time.
Worked Example
Calculate the instantaneous velocity at
Explain why using a large triangle reduces the percentage uncertainty in your answer.
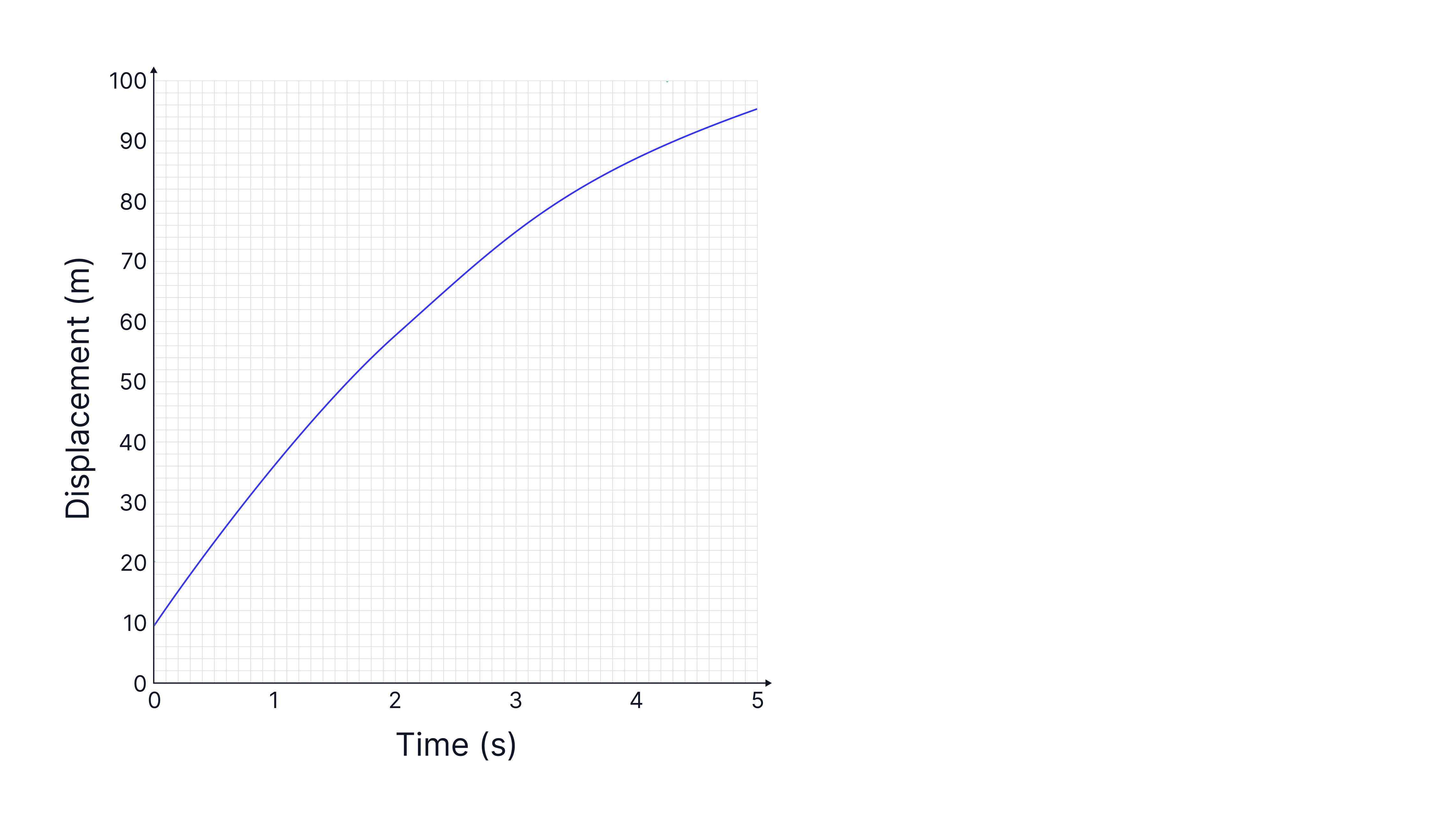
Answer:

We want to use as large of triangle as possible. If we were to determine the height of one side of the triangle was instead of its actual value of , we would be off the actual value (%). But if we used a larger triangle and determined the height of one side was instead of its actual value of , we would be off (%). Therefore, by using larger values, we are reducing the percentage uncertainty in our results.
Velocity-time Graphs
The gradient of a velocity–time graph determines the acceleration as, .
The area under a v-t graph determines the displacement as, .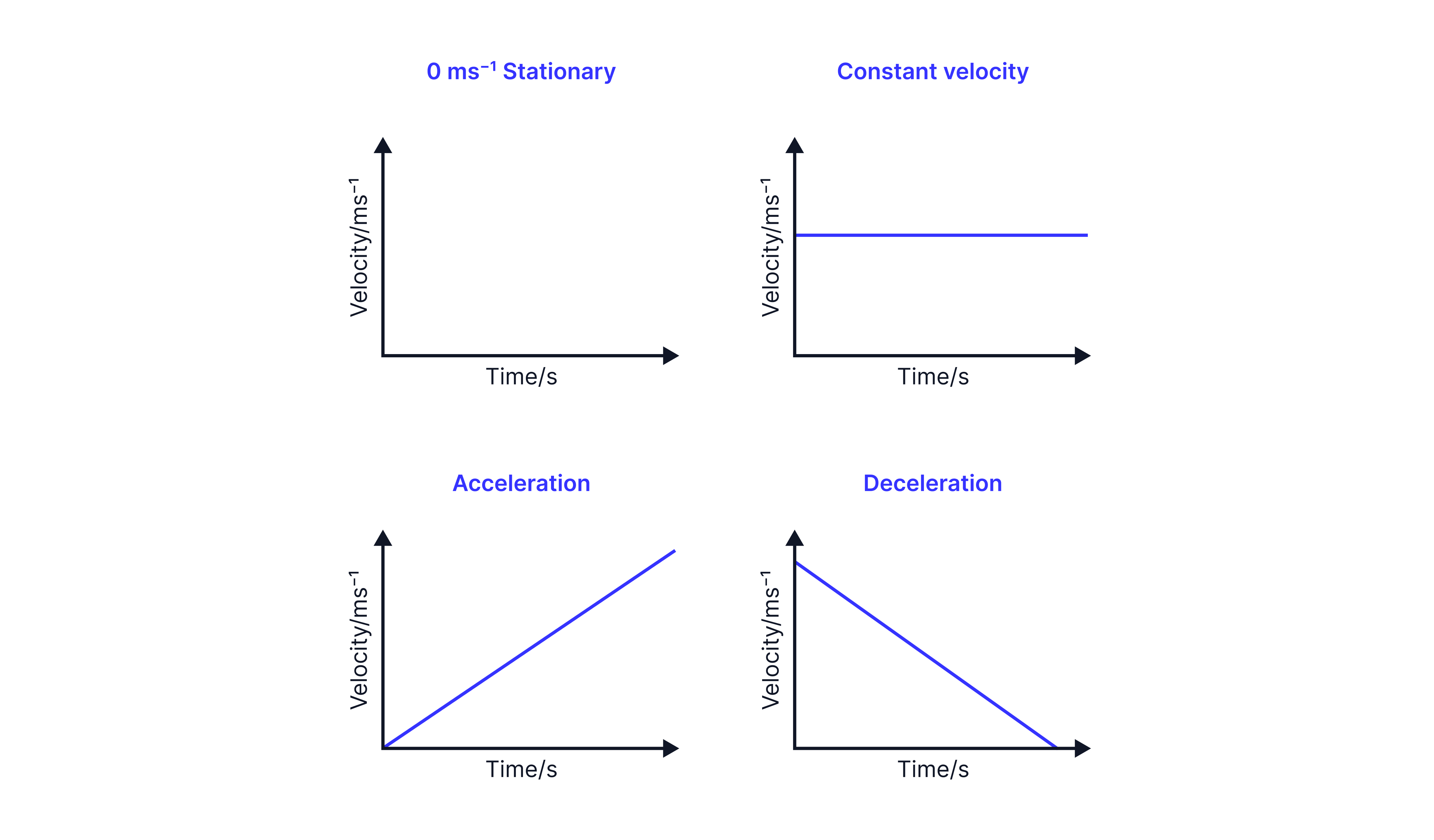
Worked Example
Describe the journey and calculate the total displacement.

Answer:
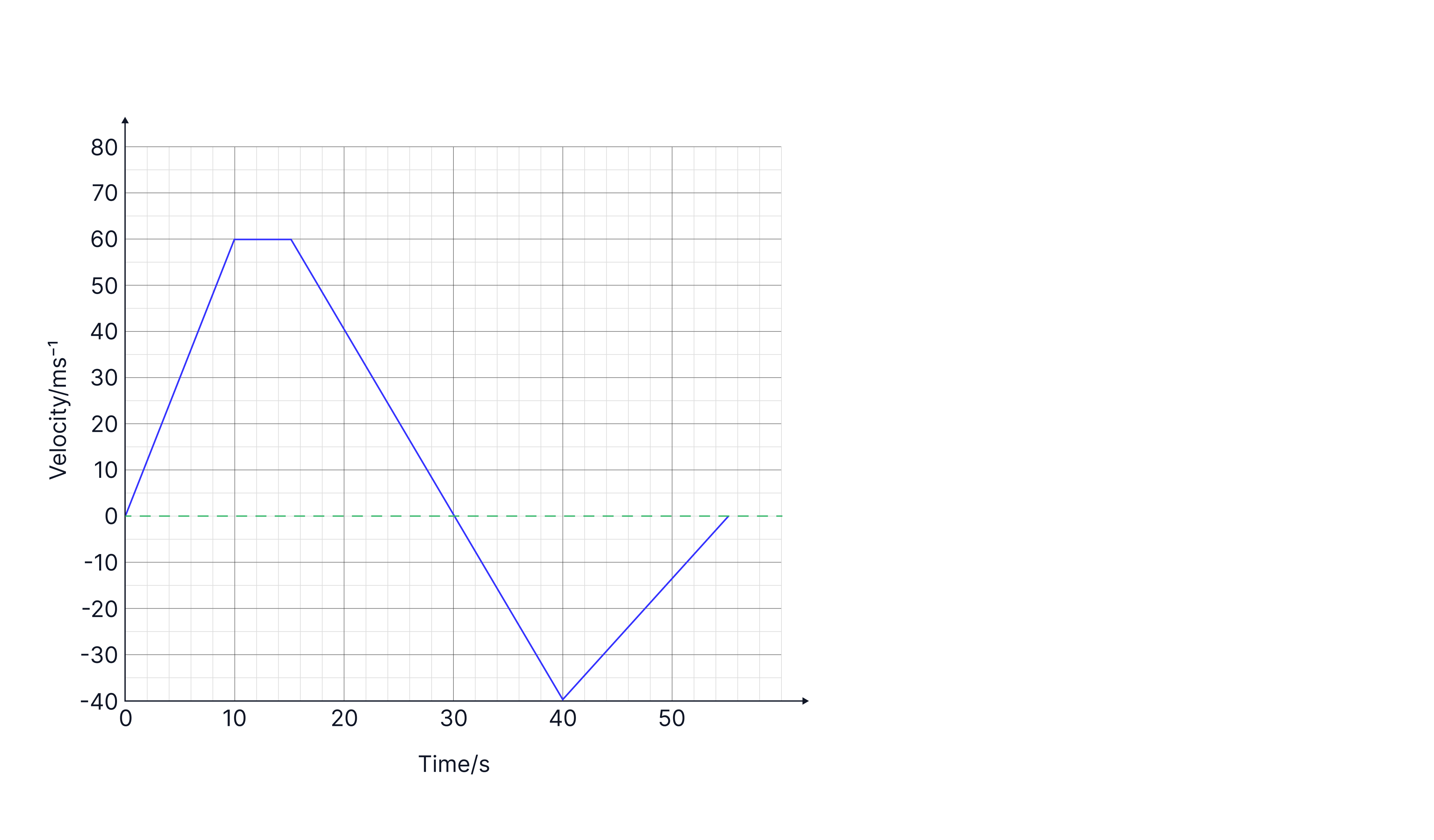
Constant acceleration of for seconds.
Constant velocity of for seconds.
The object is slowing down, decelerating from seconds to seconds . It then changes direction, increasing in speed for the next seconds, , here the negative sign implies direction rather than a drop in speed.
The object decreases in speed from to seconds, decelerating,.
The object travels a total distance in the forward direction from 0 to seconds of (area under the graph), then in the negative direction. The total displacement (distance from starting position) is in the positive direction.
Worked Example
The v-t graph for a falling ball is shown below:

Which a-t graph below shows the motion of the same ball?

Answer:

The velocity is increasing rapidly at the start as the gradient is high, which tells us there is a large acceleration. The gradient becomes less steep, but the velocity is still increasing, so the object is still accelerating, but at a slower rate. The velocity eventually becomes constant, so it is no longer accelerating, and the acceleration is zero. Therefore, overall the acceleration begins high and drops to zero over time.
Practice Questions
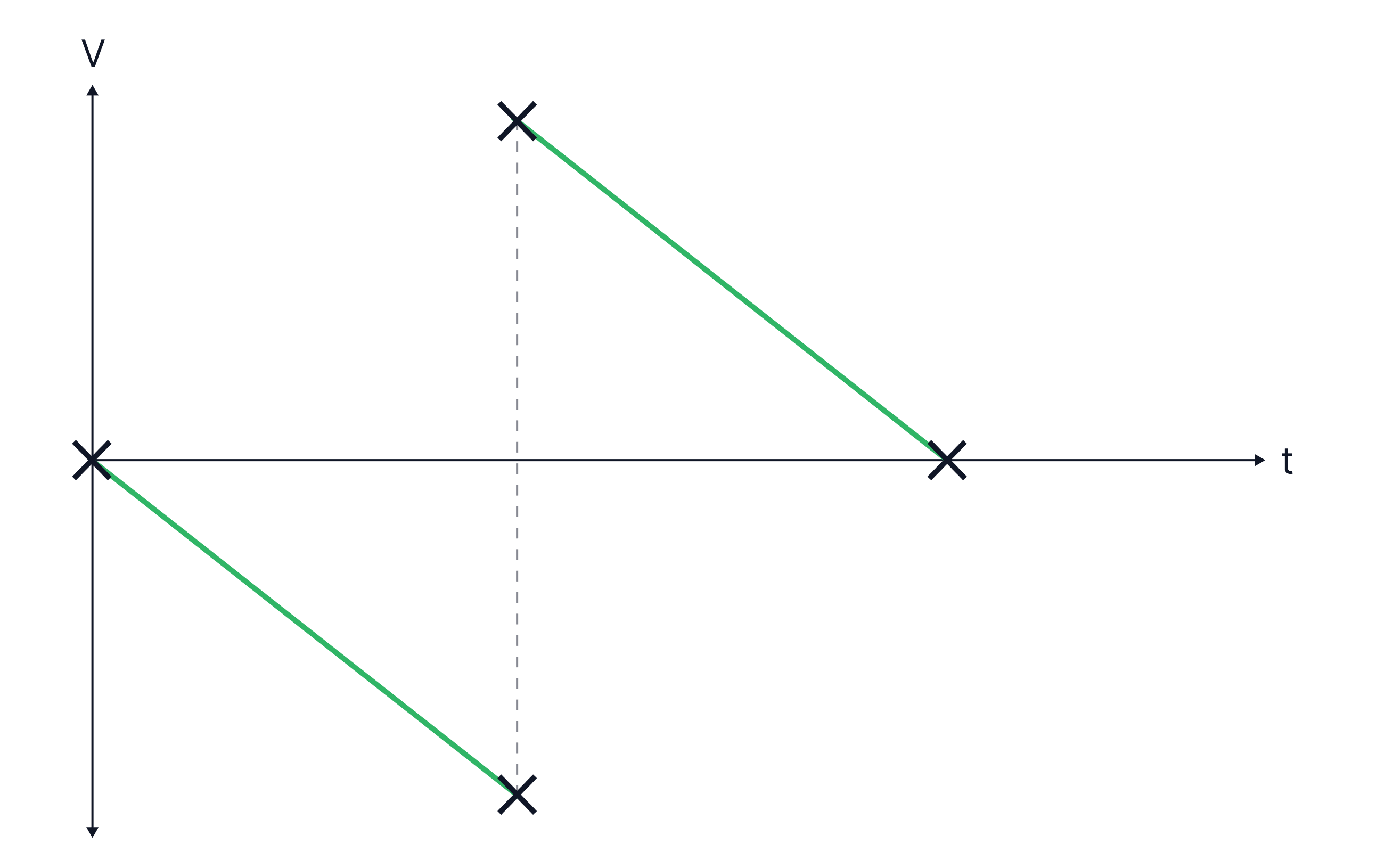
Sketch a v-t graph for a ball released from rest, falls down and then then bounces up.
Take downwards as negative motion.
-> Check out Brook's video explanation for more help.
Answer:
Draw a v-t graph for a ball thrown up in the air and caught again.
Take downwards as negative motion.
-> Check out Brook's video explanation for more help.
Answer: