Newton's Laws Of Motion
Brook Edgar
Teacher

Explainer Video
Newton's Laws of Motion
Newton's 1st law -> An object will remain at rest or continue to move at a constant velocity unless acted on by a resultant force.
Newton’s 2nd law -> , the acceleration of an object is directly proportional to the resultant force acting on the object and inversely proportional to the mass of the object.
Formula:
Inertia is the natural tendency for an object to resist changes to its motion. A stationary object will remain at rest, or an object in motion will continue to move at a constant velocity until it is acted on by a resultant force.
Worked Example
The body is accelerating as shown. Find the magnitude of the unknown forces.
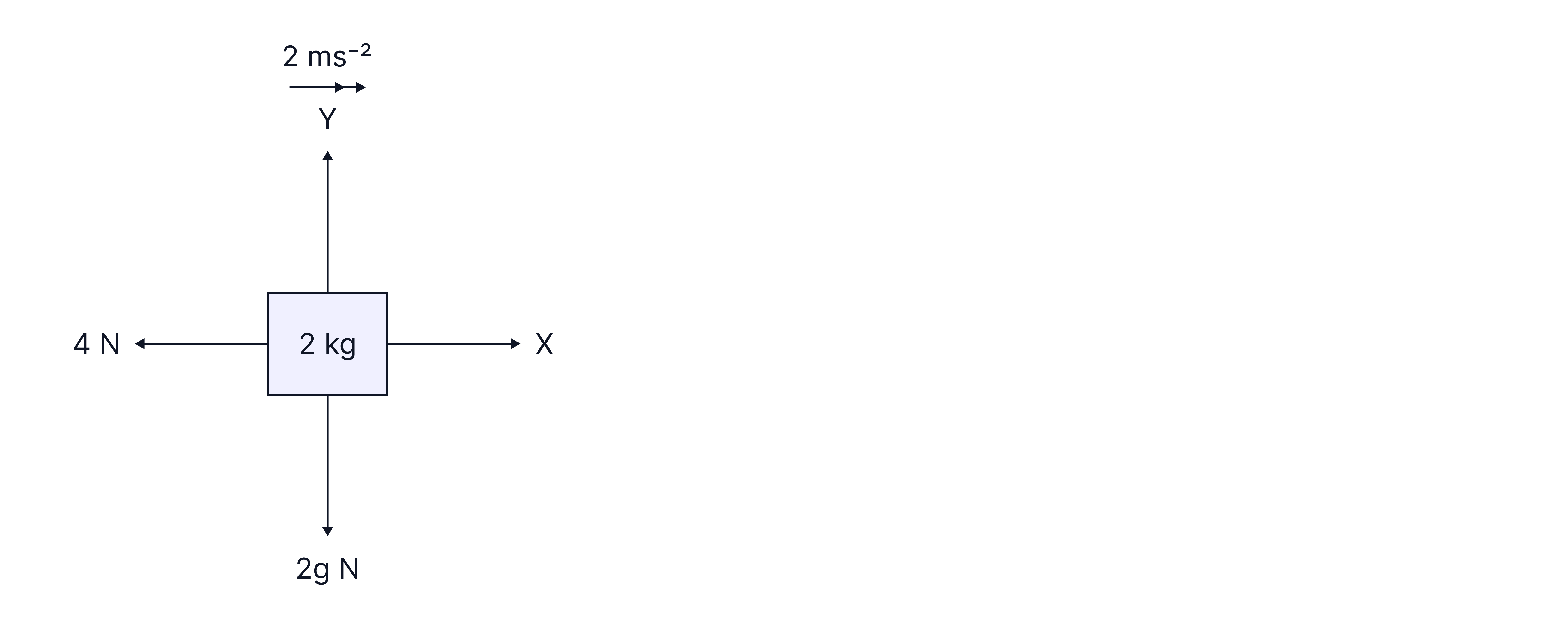
Answer:
The box is only accelerating in the horizontal direction. Therefore, in the vertical direction, the forces are balanced. (Since the acceleration is zero, the resultant force is zero, .) The upward force Y exactly equals the downward force of .
As the object is accelerating to the right, there is a resultant force:
The object has a force of to the left, so if there is a resultant force of to the right as the object is accelerating to the right, force X must be larger by four newtons,
Worked Example
A box of mass is pulled along a rough horizontal table with a force of . Opposing the motion is a constant frictional force of . Given that the box was initially at rest, calculate:
The acceleration of the box.
The distance travelled by the box in the first 4 seconds.
Answer:
Always sketch a diagram to help you visualise the problem:

Teacher Tips: In question two, we can use SUVAT as the acceleration is constant.
You are also required to resolve forces that are not in the same line of action to calculate the resultant force on an object or to separate a resultant force into its horizontal and vertical components.
These questions require an application of trigonometry.
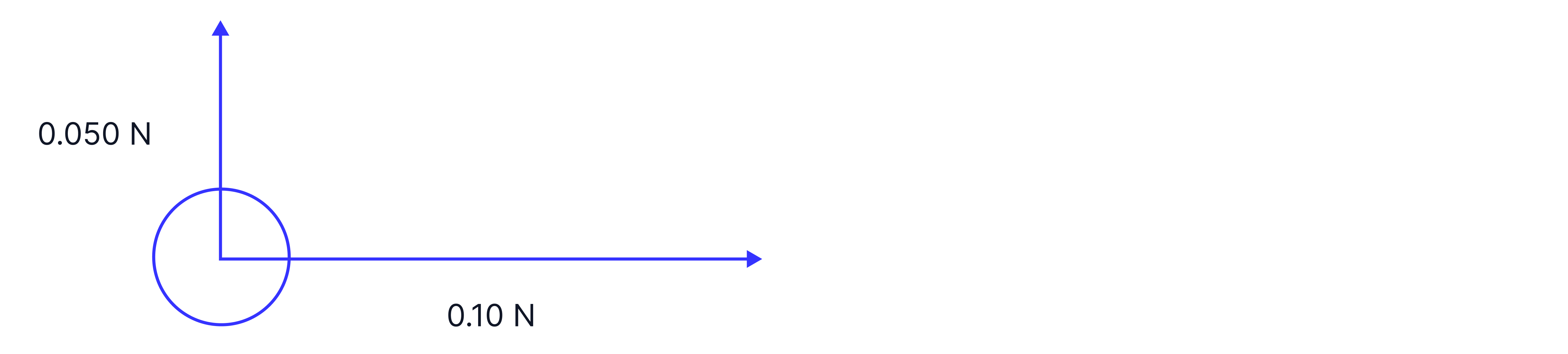
For example, if we have two perpendicular forces acting on the ball shown below, to find the resultant force, we need to redraw the forces so that the force arrows are drawn tip to tail.
We can redraw the horizontal force at the top of the vertical force to see the direction of the resultant force.
Note: If an object is in equilibrium when a diagram of resultant forces is drawn, they will always form a closed shape.
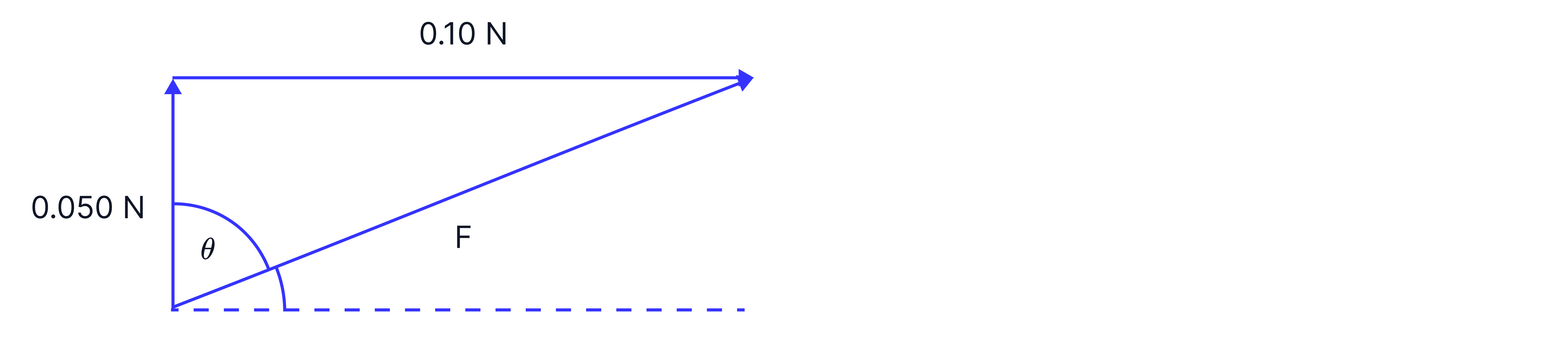
If the diagram were to scale, we could use a ruler to determine the size of the resultant force, but if not, we can use Pythagoras' theorem, .
To find the direction, we can use SOHCAHTOA to remember the trigonometric ratios.
In physics, we reference the angle above or below the horizontal. In this case the force is above the horizontal.
above the horizontal.
The next example requires us to separate the force into its components. For this box on a slope, we want to determine the force pulling the box down the slope -> the force parallel to the slope, in order to calculate the acceleration of the box down the slope. In this example, we have a box mass, , on a slope. We know that weight pulls objects straight down, so to determine the force acting on the box down the slope, we will need to resolve the weight into its parallel and perpendicular components to the slope.
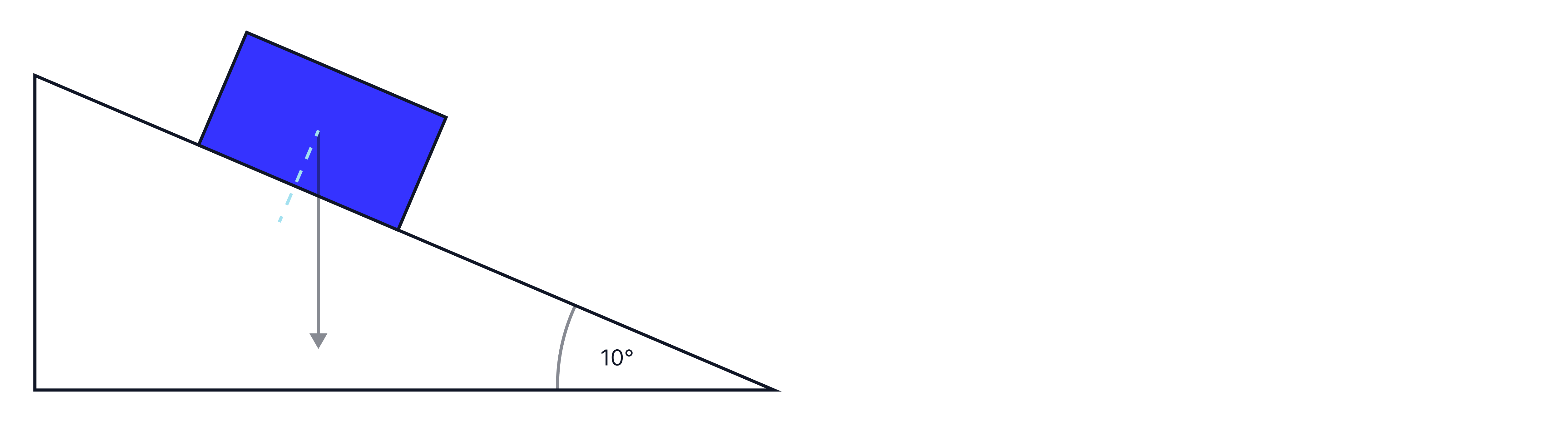
We can use the rules of triangles to label the angles we need to use in our calculations:
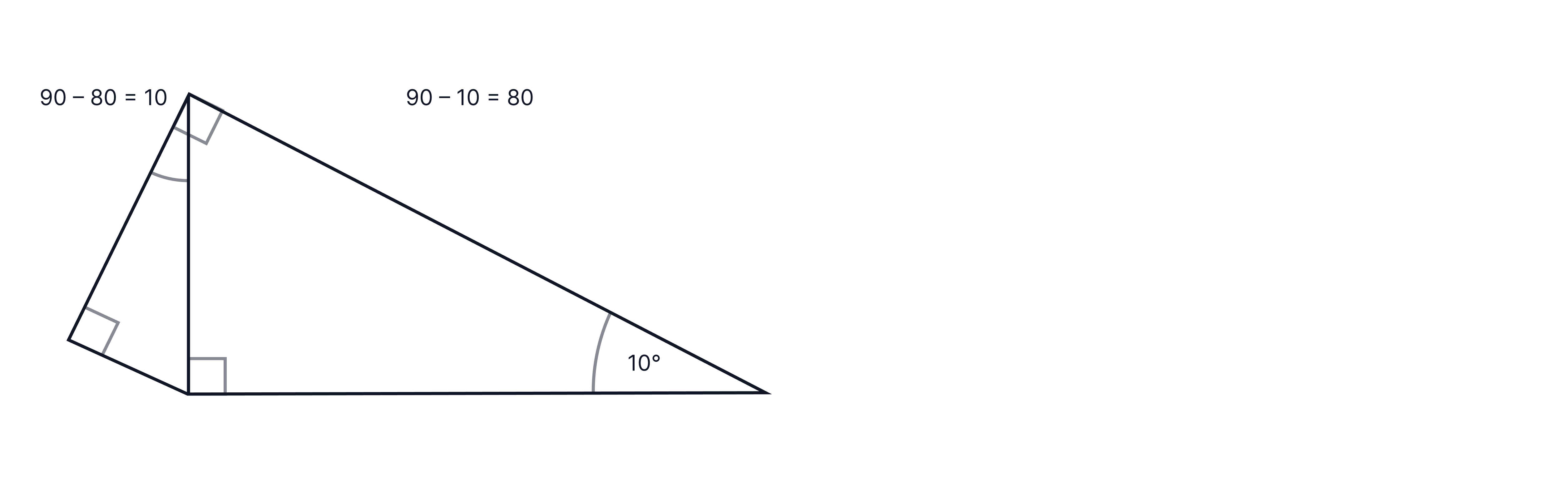
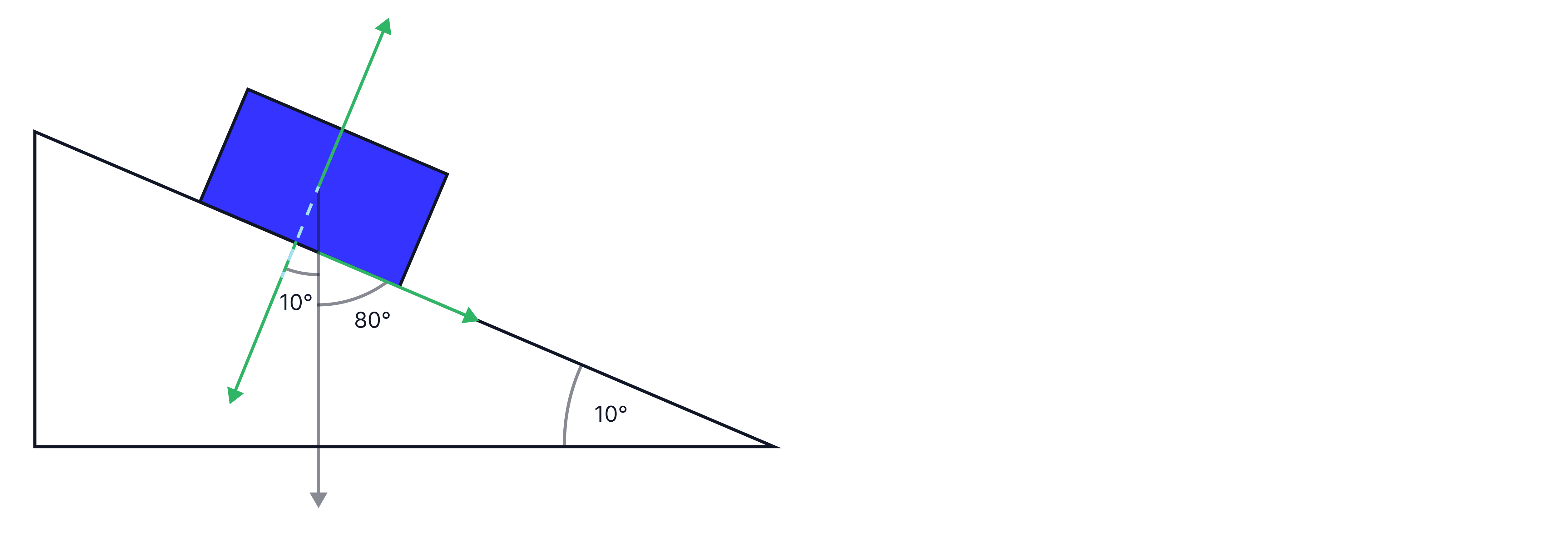
We can now determine the component of weight that acts down the slope(i.e. parallel to slope):
We could also solve for the normal reaction force if asked, as we know that the box is not accelerating in this direction, so the resultant force is zero perpendicular to the slope. Therefore, the normal force on the box is equal to the perpendicular component of weight to the slope.
Worked Example
A box has a mass of and slides down a slope, inclined at above the horizontal at .
Calculate the resultant force on the box.
Calculate the size of the friction on the box.
Answer:
First, make a sketch of the problem, labelling all relevant angles and the three forces acting on the box: weight, normal reaction force and friction.
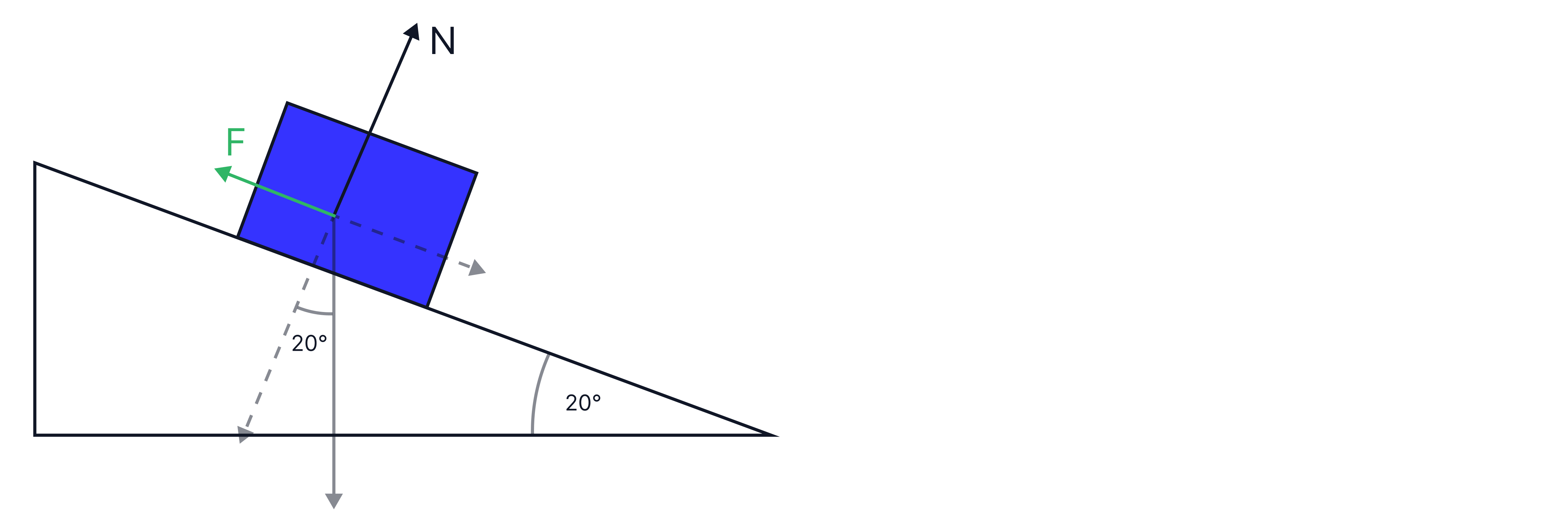
Teacher Tips: For question two, as the box is accelerating down the slope, the component of weight parallel to the slope is larger by ten newtons, 10 = parallel component of weight - friction. Parallel component of weight = .
Newton's 3rd law
When object A exerts a force on object B, object B exerts an equal and opposite force on object A.
Similarities between Newton's 3rd law pairs:
Same magnitude of forces
Same type of forces
Differences between Newton's 3rd law pairs:
Forces act in opposite directions
Forces act on different objects
For example, if we have a toy car like that in the image, propelled forward by a deflating balloon, we know from Newton’s 3rd Law that as the balloon deflates, pushing the air inside forward, the air pushes the balloon backwards with an equal and opposite force on the balloon.
Newton’s 1st Law shows us that if we look only at the forces acting on the balloon, there is a resultant force acting backwards on the balloon, caused by the air pushing back. The balloon will then accelerate in the direction of the resultant force, taking the car attached to it with it.

Worked Example
Which is an example of Newton’s 3rd law pair:
A) The man is pulled down to Earth by gravity with a force of .
The man is pushed up by air resistance by a force of .
B) The man is pulled down to Earth by gravity with a force of .
The Earth is pulled up by the man due to gravity with a force of .

Answer:
B
Newton’s 3rd law is demonstrated here as the forces are:
Equal
Opposite
Acting on different objects (man and earth)
Same type of force (Force of gravity)
Practice Questions
Resolve these vectors.
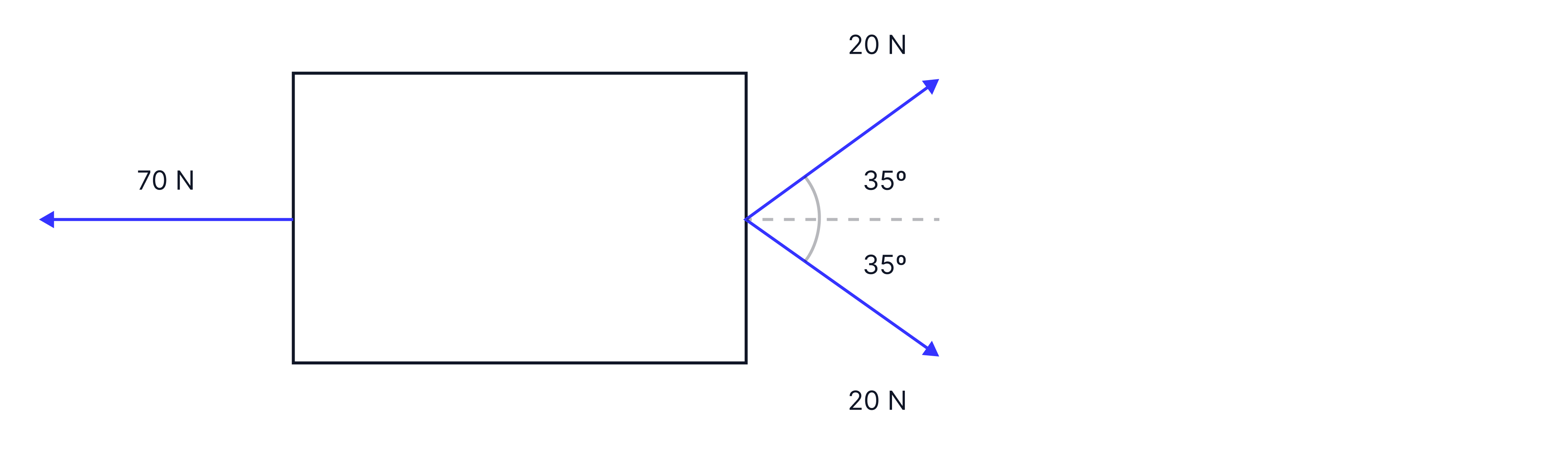
-> Check out Brook's video explanation for more help.
Answer:

Resolve these forces to calculate the resultant.
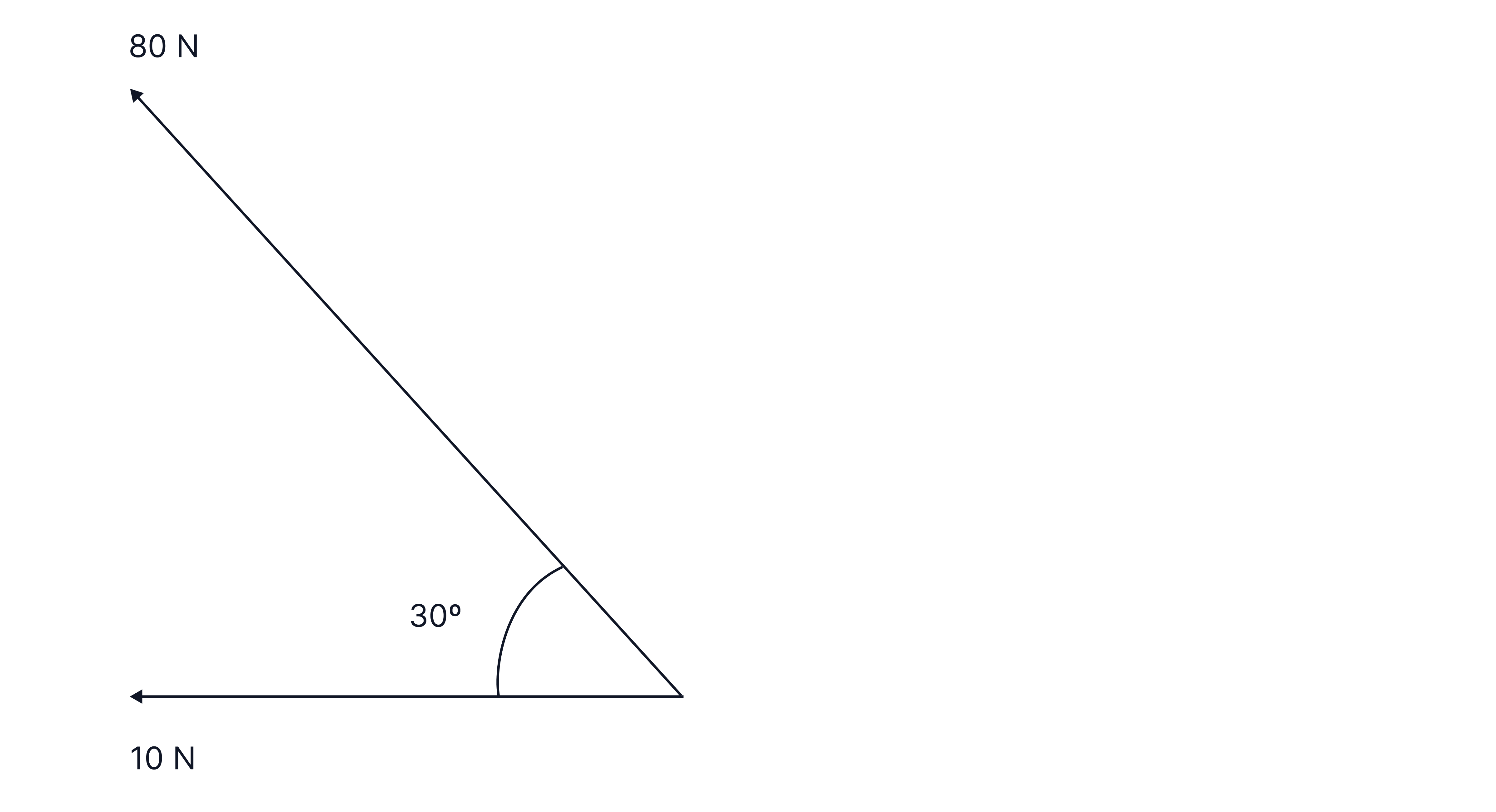
-> Check out Brook's video explanation for more help.
Answer:
above the horizontal.
The system below is in equilibrium.
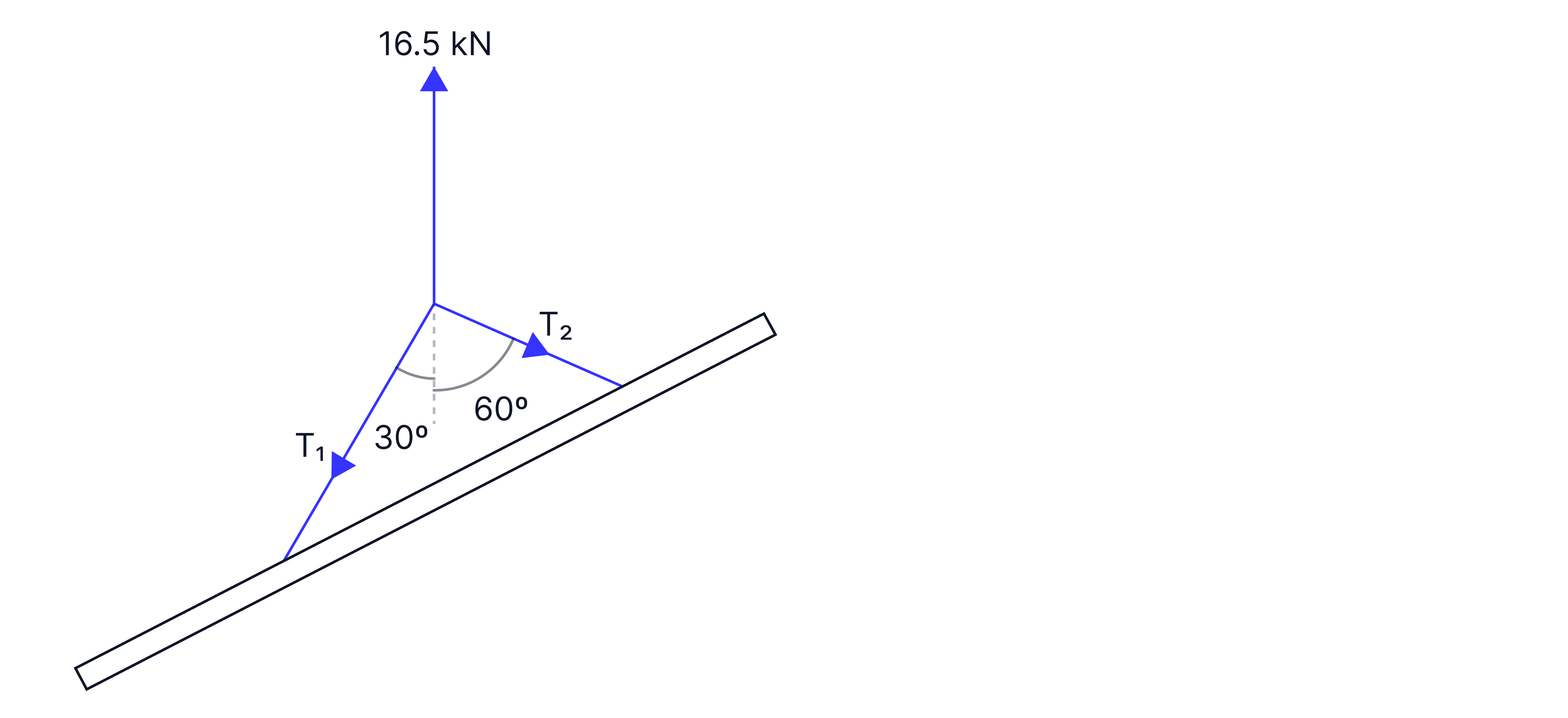
Find .
Find .
-> Check out Brook's video explanation for more help.
Answer: