Photoelectric effect
Brook Edgar
Teacher
Explainer Video
Photoelectric effect
People knew that light was a wave because it diffracts, as seen in Young's double-slit experiment. As light is an EM wave of continuous energy, it was thought that when shone onto a metal’s surface, electrons in the surface of the metal would absorb energy from the wave until they had enough energy to be freed.
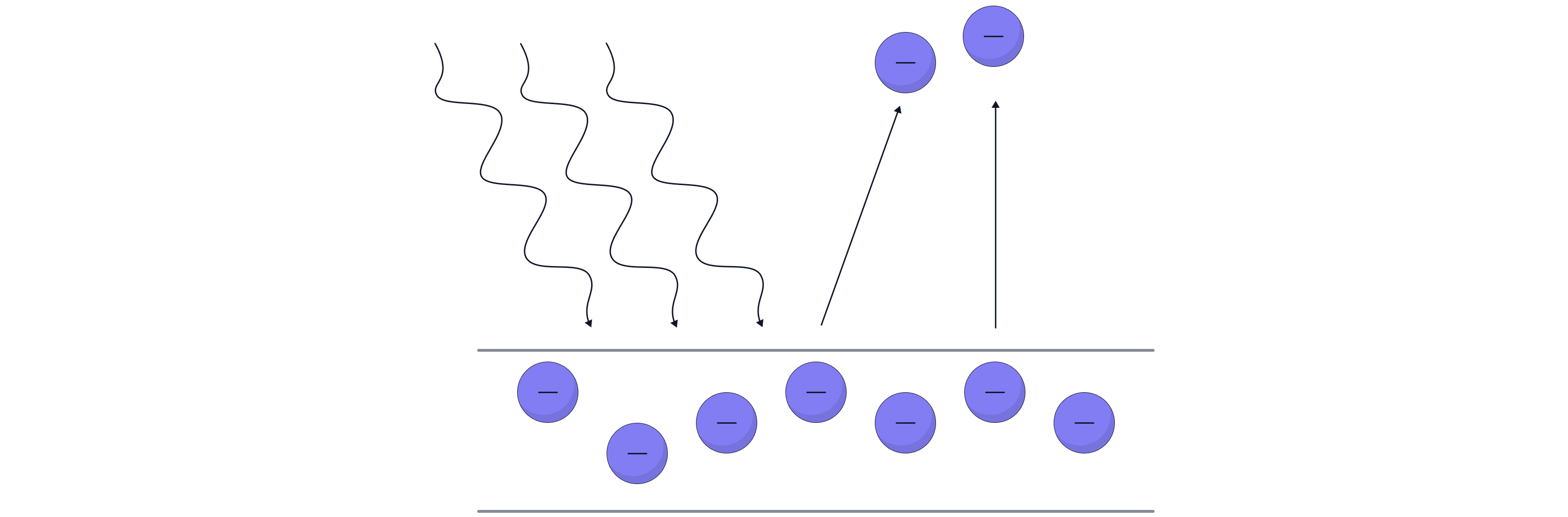
However, it was observed that when light was directed at the metal's surface, either the electrons were emitted instantaneously or not at all. This showed that electrons do not continuously absorb energy from the wave, but rather that they only absorb energy and are emitted if the light's energy exceeds a certain threshold value. This minimum energy is known as the work function, . From the observed results, Einstein proposed that light came in discrete packets of energy, called quanta, also known as photons, as electrons were only emitted when the frequency of the light exceeded a certain threshold frequency.
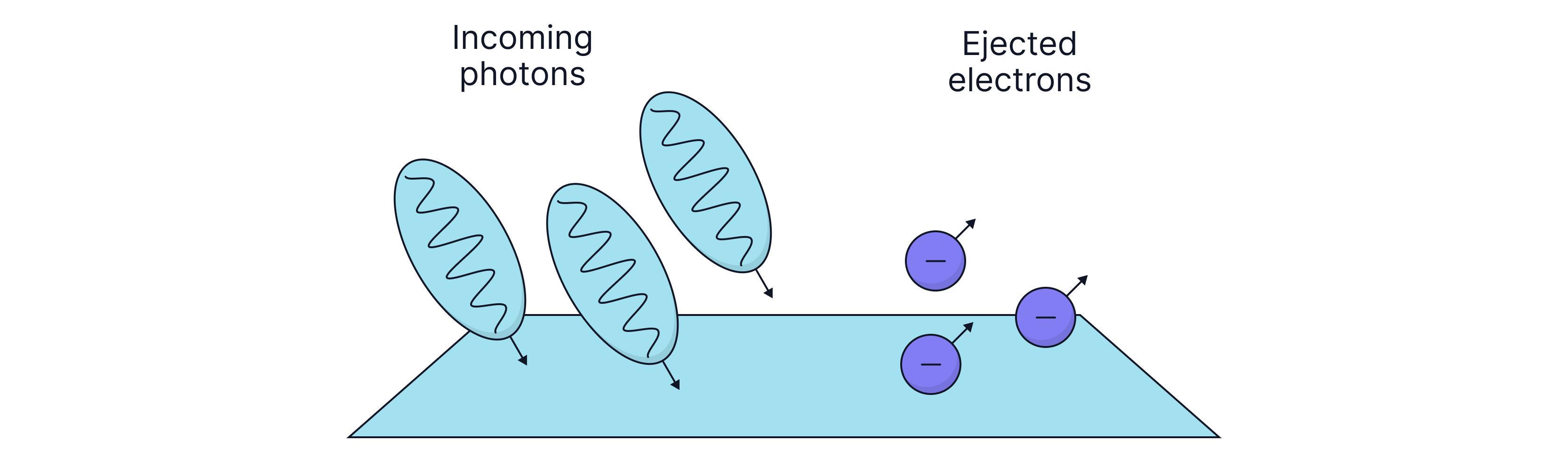
It was also observed that it was a interaction between the electron and photon – Einstein was awarded a Nobel prize for this discovery. He explained that light can also behave as a particle.
The electrons emitted from the surface of the metal are known as photoelectrons, and this experiment is known as the photoelectric effect. If the energy of the incident photon is , then the extra energy is given to the kinetic energy of the photoelectrons.
Mathematically, the photoelectric effect can be written as:
Formula:
The energy of the incident photon can be calculated using the equation below:
Formula:
If we increase the intensity of light, we are directing more photons per second at the metal's surface. As long as the energy of each photon is above the work function of the metal, as it is a interaction, more photons = more electrons.
Worked Example
Light of wavelength is incident on a metal with work function . Calculate the speed of the fastest emitted electron.
Answer:
First, we need to calculate the energy of the light to see if it is above the work function of the metal.
We need to convert the energy of the work function of the metal from electronvolts, eV, into joules.
As the energy of light is greater than the work function of the metal, photoelectrons will be emitted. We now can calculate the maximum kinetic energy they will be emitted with.
Using the mass of an electron from the formula sheet, we can now calculate the speed of the electron.
Teacher Tip: An electron volt is a way to write energy when the energy values are extremely low.
Worked Example
Light of wavelength is incident on a metal with a work function of .
Determine if electrons will be emitted from the surface of the metal and if so, what will be the fastest speed of the electrons?
Determine the longest wavelength of light which could cause photoelectric emission from this metal.
Answers:
The energy of the light is less than the work function of the metal no electrons are released.
We need the energy of light to be greater than the work function for the photoelectric effect to occur. The longest wavelength of light will be the least energy required to get photoemission, which is the work function.
Work Function
The setup below can be used to determine the work function of a metal. The minimum energy required to free an electron from the surface of a metal.
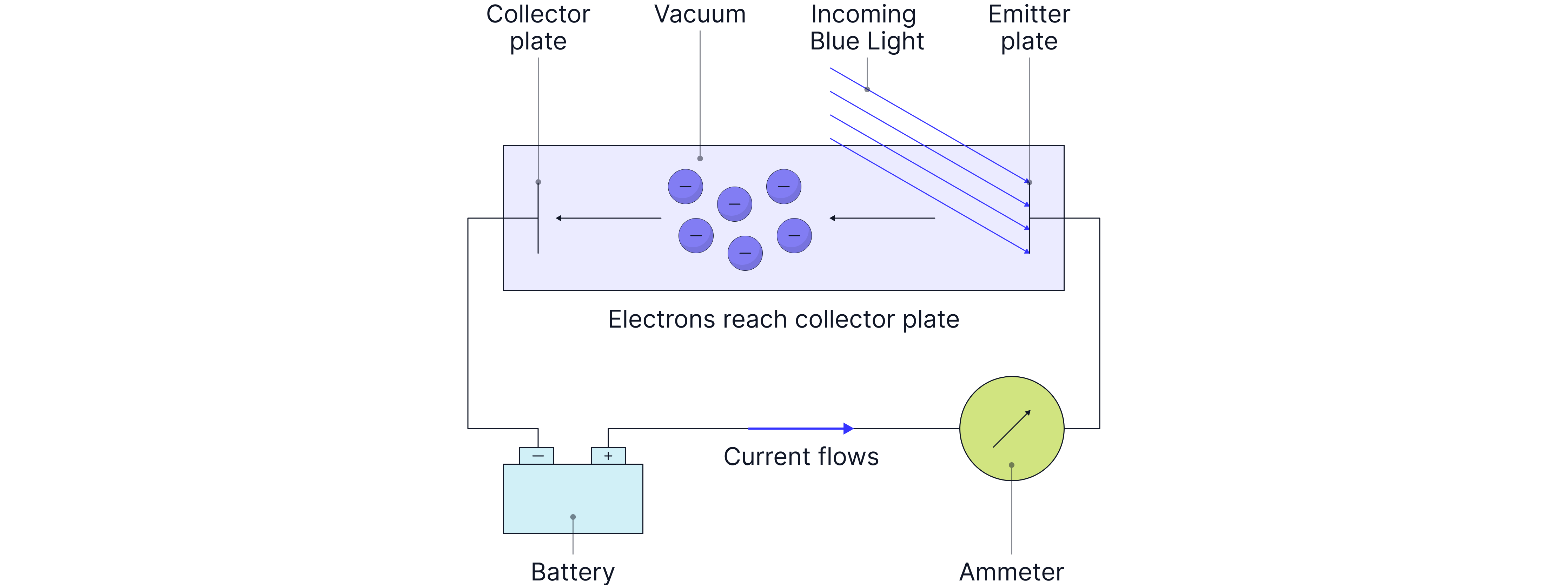
Light is shone on the metal plate. If a current is detected on the ammeter, we know that the energy of the light is greater than the work function, as electrons are then freed from the surface of the metal plate and can travel across the gap to reach the collector plate, completing the circuit.
As the potential difference (pd) across the plates is slowly increased, fewer and fewer electrons will reach the collector plate, as they will need an energy, E = Vq, to cross the gap. When the current drops to zero, the kinetic energy of the fastest-moving electron is less than the energy between the plates due to the pd applied. This potential difference is known as the stopping potential and is used to determine the work function of the metal, provided we know the energy of the light and the potential difference between the plates when the current drops to zero.
For example, if the current drops to zero when the pd across the plates is , we then know the kinetic energy of the fastest-moving electron, as at no electrons have enough energy to cross the gap between the plates. If light of wavelength is shone on the plate, we can calculate the energy of the light and thus the work function of the metal.
Worked Example
Sketch a graph of maximum kinetic energy against frequency and state what information can be determined from the graph.
Answers:
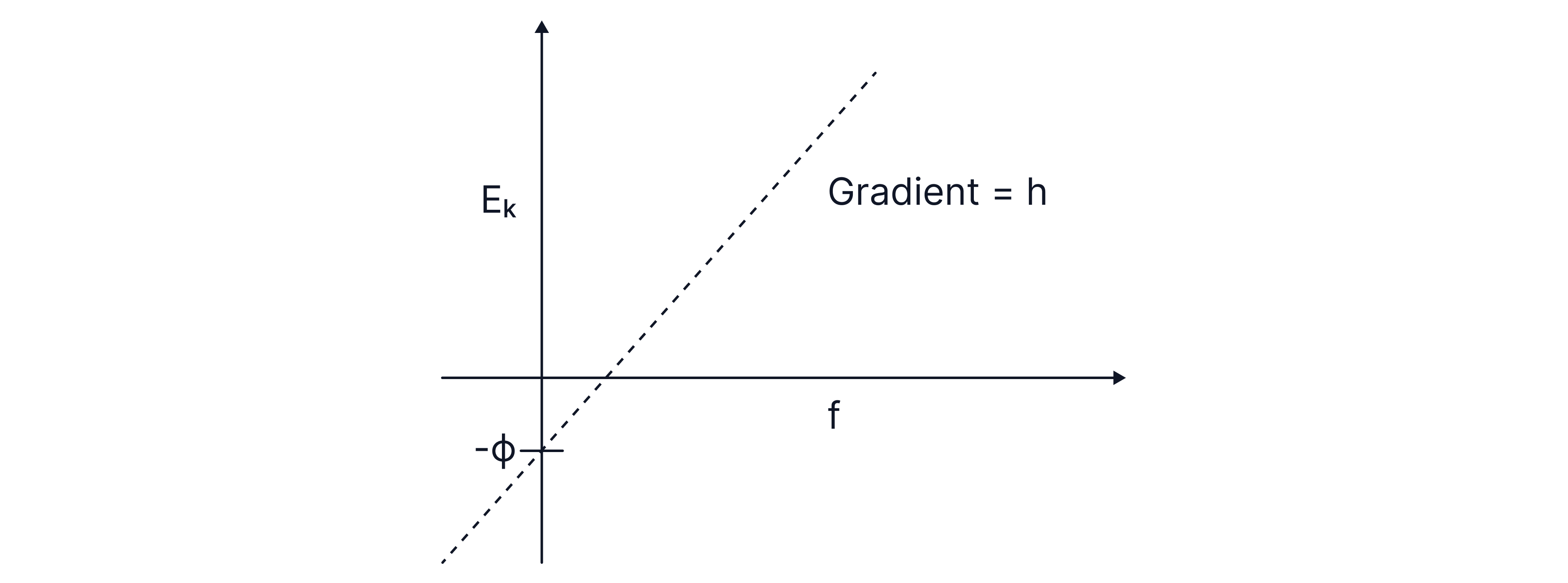
Comparing the equation with , we can see that the gradient = Planck's constant, , and the y-intercept = negative work function, .
Worked Example
For these questions, remember to talk about frequency, stopping voltage, and maximum .
Describe (including numbers) what graph A shows.
Describe (including numbers) what graph B shows.
Answers:
As the frequency of light increases, a higher stopping voltage is required for the current to reach zero, meaning that electrons are emitted with greater kinetic energy as a greater pd between the plates is needed to stop them. Increasing the frequency of light doesn’t affect the size of the photocurrent (number of electrons emitted per second), it remains at , as the frequency of light doesn't affect the number of electrons emitted per unit time, as it is a 1:1 interaction.
Higher light intensity means more electrons are emitted per unit time as the photocurrent increases, as more photons per second hit the surface, resulting in more electrons emitted per second, as it is a 1:1 interaction. The stopping voltage remains the same at ~ , showing that the maximum kinetic energy of the photoelectrons is not affected by changing intensity.
Practice Questions
Explain how the photelectric effect shows the particle properties of light.
-> Check out Brook's video explanation for more help.
Answers:
Electrons are only emitted from the surface of the metal if the energy of light is above a certain threshold value known as the work function. This shows that light is not a continuous wave of EM energy, as otherwise the electrons could absorb energy from the light wave until they have enough to be emitted from the surface of the metal. Also, electrons are emitted instantaneously or not at all, showing again that the electrons can not accumulate energy from the wave, as otherwise they could get emitted later. It is a 1:1 interaction, indicating that one photon causes the emission of one electron.
Photoelectrons are released when monochromatic light with photon energy is incident on a metal surface with a work function of .
Calculate the maximum speed of the photoelectrons as they leave the surface.
-> Check out Brook's video explanation for more help.
Answer: