Thermal Equilibrium
Brook Edgar
Teacher

Explainer Video
Thermal Equilibrium
When two substances are brought into contact, their temperatures change until thermal equilibrium is reached. Heat always transfers from the hotter to the cooler object.
This explains why, when you take a can out of the fridge, the temperature of the liquid inside increases. Its temperature rises until it comes into thermal equilibrium with its surroundings. Droplets of water can be seen running down the side of the can as the warm air in contact with the cold surface cools and condenses, forming water droplets.
We can use specific heat capacity and specific latent heat of substances to determine the final equilibrium temperatures reached.
For Example, if of ice at is dropped into a bucket containing of water at we can calculate the final equilibrium temperature reached by equating the total loss in energy of the water to the total energy gain of the ice.

Specific latent heat of fusion of ice =
Specific heat capacity of water =
Specific heat capacity of ice =
First we calculate the energy change as the ice at increases in temperature to .
Then the ice at it must then change state to water at .
The water at then increases in temperature to the final equilibrium temperature, T.
Finally we know that the water at will decrease in temperature to the final equilibrium temperature, T.
Remember: For temperature change -> you always subtract the higher temperature from the lower, not always final–initial, as you want a positive number inside the brackets. So, if the substance drops in temperature, you will calculate the starting temperature minus the final temperature to obtain a positive value.
To finish we equate the total energy losses to the total energy gains, as the total gain in energy of the ice comes from the loss in energy of the water.
Worked Example
Coke at , mass , is poured into a glass, mass , initially at .
Calculate the final temperature of the drink when it reaches thermal equilibrium with the glass.
Specific heat capacity of glass =
Specific heat capacity of coke =
Answer:
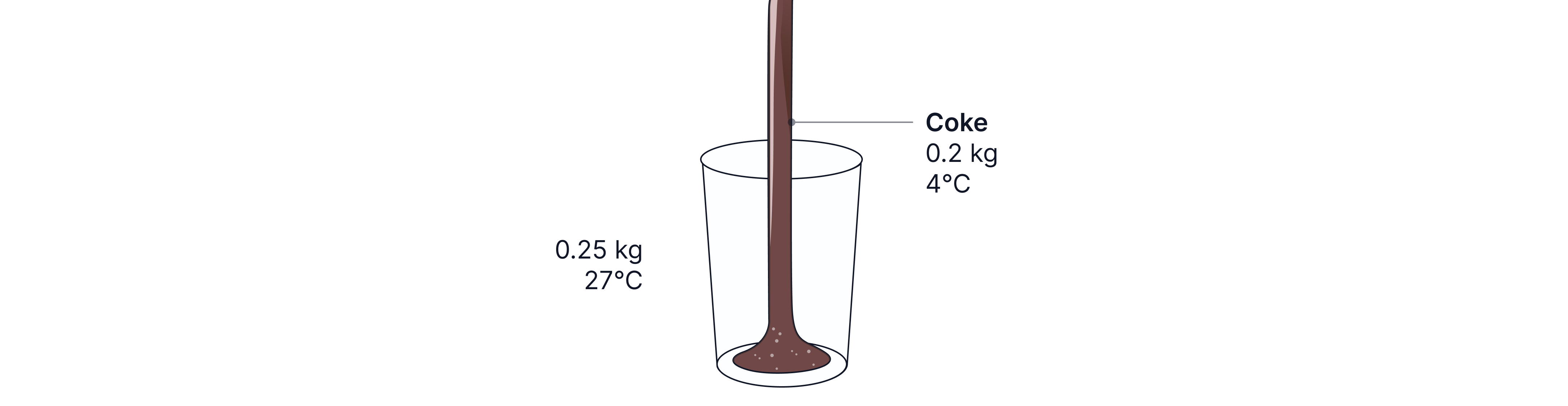
The coke increases in temperature to some final temperature, T.
The glass decreases in temperature to some final temperature, T.
Finish by equating total energy loses and energy gains.
Teacher Tips: Remember, when calculating the change in temperature inside the brackets, always use the higher number minus the lower. We know the coke increase in temperature, so the final temperature, T, reached is higher than the initial temperature of . Hence, why it is . The water drops in temperature, so the initial temperature, will be higher than the final temperature, T. Hence, why it is .
Worked Example Continued
Ice at is then added to the glass cooling the whole drink from to . Determine the mass of ice added to cause this change.
Specific heat capacity of coke =
Specific heat capacity of water =
Specific latent heat of fusion of ice =
Answer:

The coke decreases in temperature to .
The glass also decreases in temperature to as thermal equilibrium is reached.
The ice added will first melt, changing state from ice at to water at and then it will increase in temp to -> the final equilibrium temperature reached.
Finally we equate total energy losses to energy gains to find the mass of ice added.
Practice Questions
A student drops of ice into a bucket with of water.
Ice is initially at , water at . Calculate the final equilibrium temperature reached.
SHC Water =
SLH fusion of Ice =
SHC Ice =
-> Check out Brook's video explanation for more help.
Answer:
of ice at is dropped into a bucket of of water at . Calculate final equilibrium temperature reached.
SHC Water =
SLH fusion of Ice =
SHC Ice =
-> Check out Brook's video explanation for more help.
Answer: