Uncertainties

There are seven SI base quantities that you need to know. First introduced in Topic .

-> Mass (), Temperature (), Length (), Current (), Amount of substance (), Time () and Luminous Intensity ().

All other units can be expressed in terms of their SI base units.

For example, to write the unit for emf in terms of its SI base units, we first need to find an equation that involves the term of interest -> and rearrange to make the subject ->.

Energy is measured in joules, which is not an SI base unit, and charge is measured in coulombs, which is also not an SI base unit. we need to use two more equations to easily express these two units in terms of their SI base units.
and

Substitute in units, as current is measured in amps, times in seconds, mass in kilograms and velocity in metres per second, all SI base units, we just need to simplify now.

Resolution is the smallest change in quantity being measured. It is a measure of the equipment's sensitivity.

The resolution of a standard ruler is /. This means all readings are within . So if a value is recorded as , its actual value could be anywhere from . The resolution of the equipment tells you the absolute uncertainty of your measured value e.g. .

When recording results, you need to ensure all recorded data is to the same number of decimal places, as this tells you about the resolution of the equipment used.

We always repeat measurements because it reduces the effect of random error –> we can spot anomalies (outliers) more easily and thus ignore them from our results when calculating the mean. When we repeat a measurement, the absolute uncertainty in the mean will no longer be due to the equipment's resolution but will instead equal half the range of the measured values. The uncertainty needs to have the same number of dp as the final answer.

For example, in the table below, we can see that the experiment was repeated four times, the resolution of the equipment is , but to calculate the absolute uncertainty in the results, we find half the range of the measured values.

All data is recorded to the absolute uncertainty

To calculate the percentage uncertainty in our results, we use the equation, .

This shows that the larger the recorded value, the lower the percentage uncertainty. This is why we don’t time one oscillation but many, and why we wouldn't measure the thickness of just one piece of paper but many. The percentage uncertainty is usually quoted to two significant figures.

For example, using the data below, we want to calculate the absolute uncertainty and the percentage uncertainty in our results when determining the wire's diameter.

First, we notice that is an anomaly. We ignore this from our results.

When calculating uncertainties, we use the rules below. You need to memorise these rules!

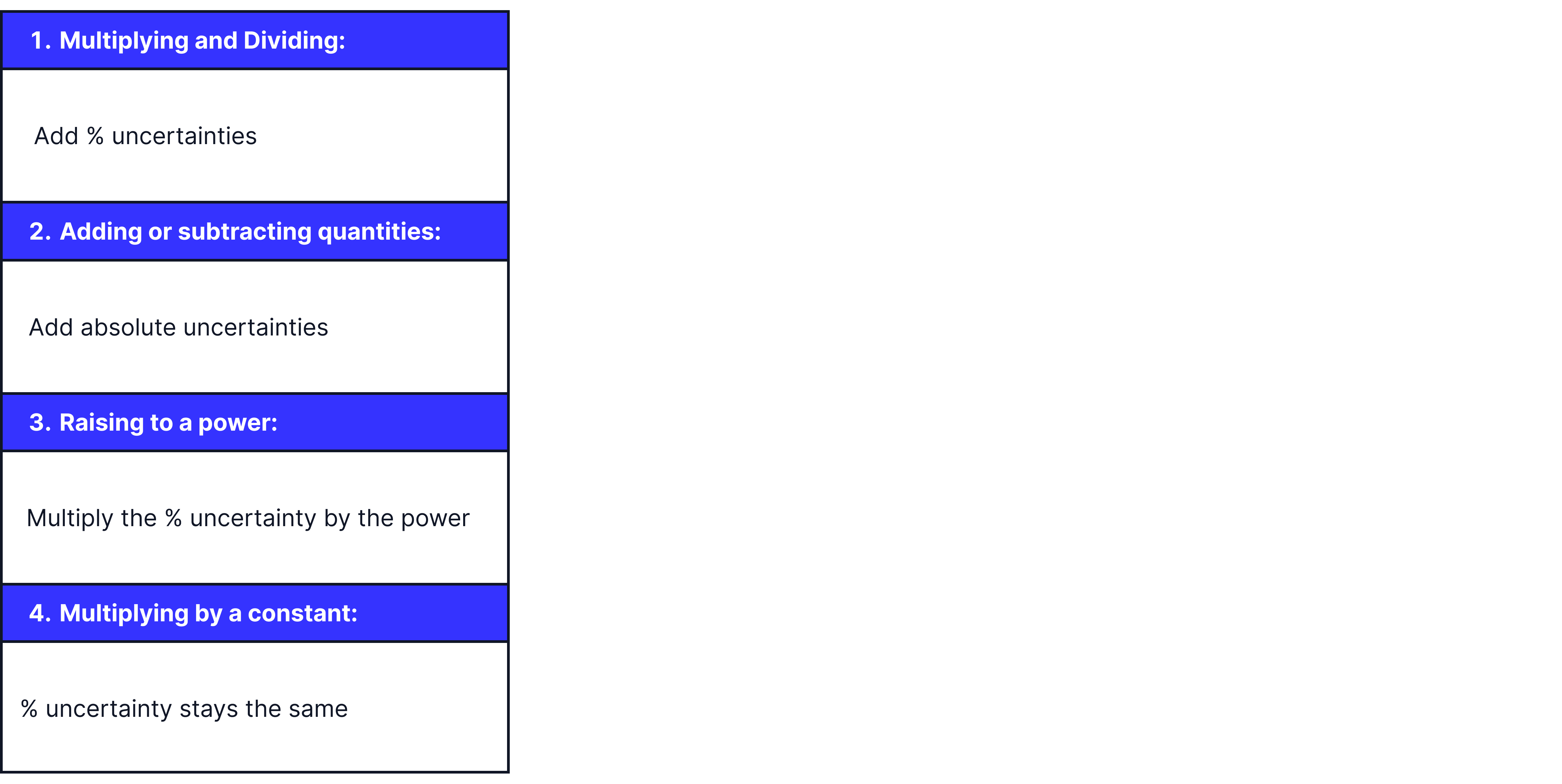
Examples:

To find , we first multiply the values to get, , quoted to the worst sf in the data (2 sf). To find the absolute uncertainty in , as we are multiplying, we need to calculate the percentage uncertainties for and and add them. We then work backwards to find the absolute uncertainty from knowing the percentage uncertainty and value.

% U in %

% U in %

% U in %

To find , we first square five, . To find the absolute uncertainty in , as we are multiplying by a power, we need to calculate the percentage uncertainty for and multiply by the power, two. We then work backwards to find the absolute uncertainty from knowing the percentage uncertainty and value.

% U in %

% U in = % U in %

Note: absolute uncertainty to have the same number of dp as the final value.