Young's Modulus
Brook Edgar
Teacher

Explainer Video
Young's Modulus
Young’s Modulus is a measure of a material's stiffness. It is defined as stress over strain.
Unit Pascal or .
Formula:
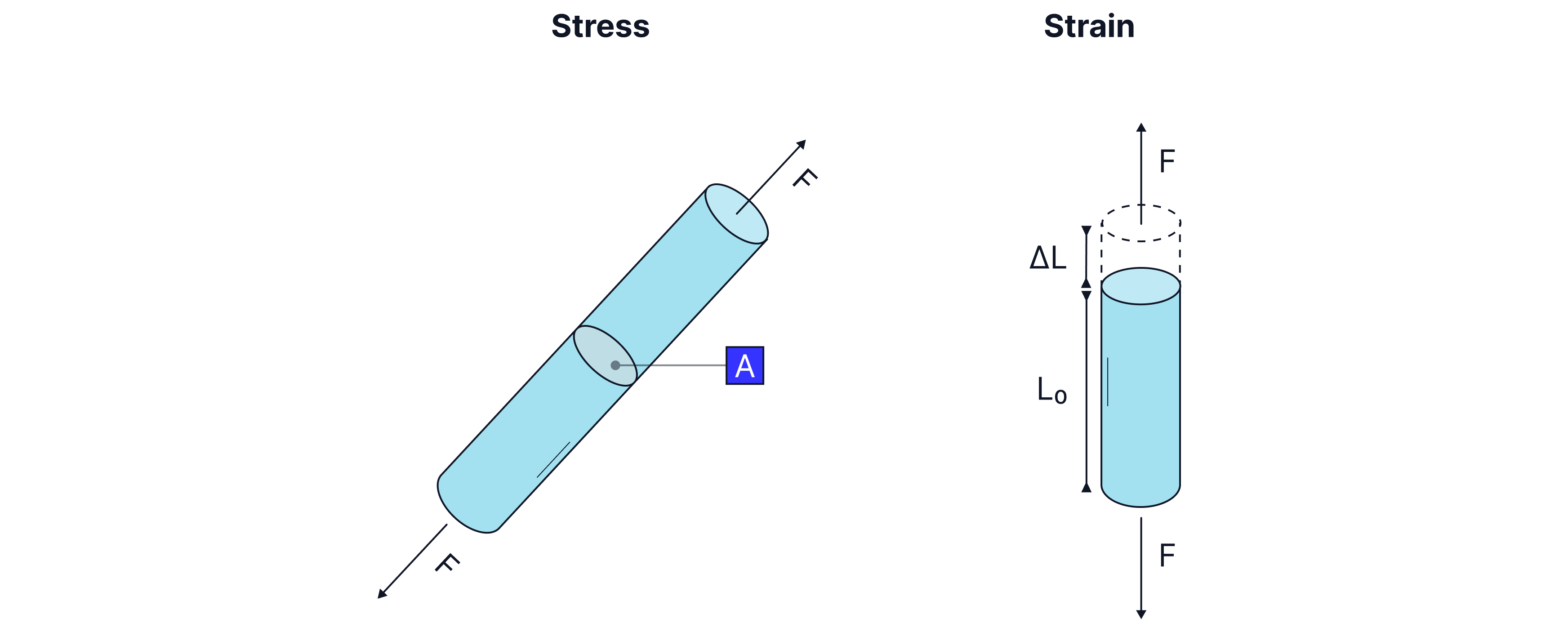
Stress is defined as the force per unit area, .
Strain is the change in length per unit length, . It has no units (it is dimensionless).
The material that is stiffer, with a greater Young’s Modulus, will have a steeper gradient as the gradient of a stress-strain graph is , which is the Young’s Modulus.

Example problem:
A wire is made from a material with Young's Modulus, . The original length of the wire is with cross-sectional area of . The wire is stretched to . Assuming that Hooke’s law is obeyed, we can calculate the tension in the wire.
We can also calculate the energy stored in the wire when extended.
Worked Example
A copper wire of length is stretched by hanging a mass on it. Given the diameter of the wire is , calculate the extension of the copper wire.
Answer:
Worked Example
Two wires and have the same dimensions but are made from different materials. Each wire’s fracture point and are shown on the graph of stress against strain.
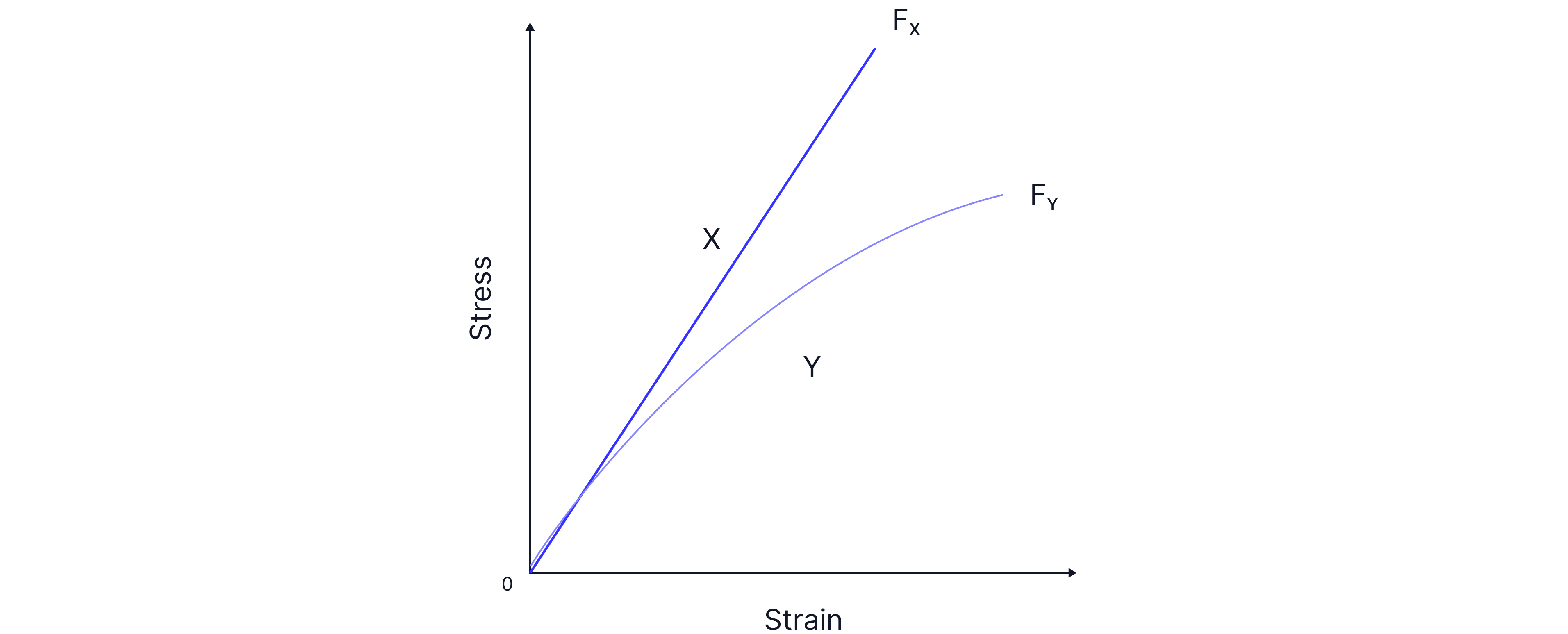
State and explain which wire or obeys Hooke’s law up until the point of fracture.
State and explain which wire or is weaker.
State and explain which wire or is ductile.
State and explain which wire or has the greater elastic strain energy for a given tensile stress.
Answer:
, as stress and strain are directly proportional for the whole graph which is shown by a straight line up until .
, as it has a lower breaking stress so fractures with less force per unit area.
, as it exhibits plastic behaviour. For a given force, it extends more.
, as for a given stress it has a greater strain, and therefore a greater extension. Using the equation, , we can see that the energy would be greater (greater area under the graph).
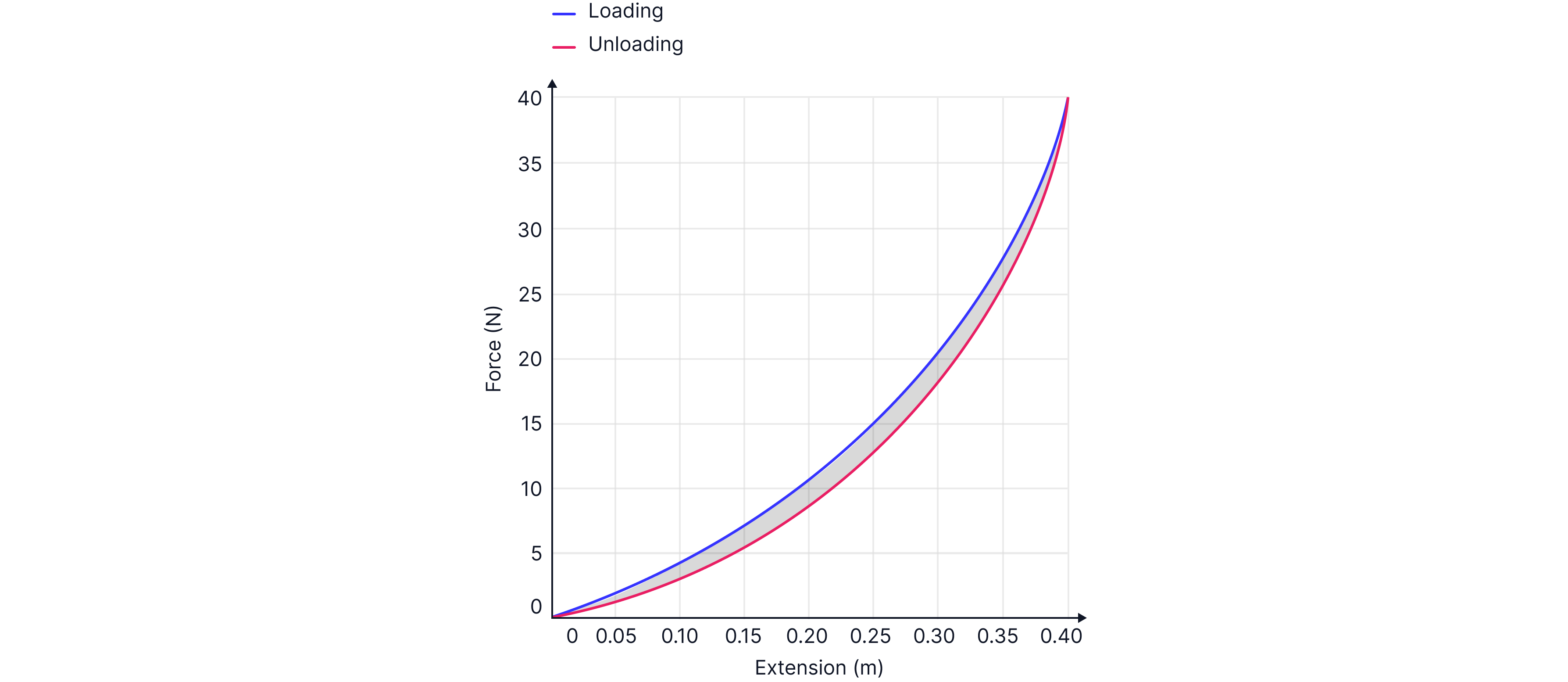
The area under a loading curve represents the energy required to stretch a material.
The area under the unloading curve represents the energy released when the applied force is removed.
The difference in the loading energy and the unloading energy is the energy dissipated as thermal energy. This is shown by the area of the shaded region (the grey area between the red and blue lines).
Remember: In exams, if we are given graphs with large boxes and we are asked to calculate the area under the graph, you would count the number of squares and multiply by the area of one square. For example if we wanted to calculate the energy released during unloading in the graph above, the area of one box is and the total number of boxes is roughly twenty. .
Practice Questions
Which cannot be used as a unit for Young's Modulus?
-> Check out Brook's video explanation for more help.
Answer:
A wire has a Young's Modulus of . A second wire is made of the same material but with three times the length and half the diameter of the first wire.
What is the Young's Modulus of the second wire?
-> Check out Brook's video explanation for more help.
Answer: