Electric Potential
Brook Edgar
Teacher

Explainer Video
Electric Potential
The electric potential at a point is defined as the work done per unit charge to bring a positive unit charge from infinity to a point in the field.
Formula:
At infinity, electric potential is defined as zero .
It is a scalar quantity.
The definition can be derived from the equation .
Formula:
The image below shows the electric potential lines around two positive charges and the direction of the electric field lines. If a proton is moved from infinity to point Z, work is done on the proton as energy is required to push the proton, which has a positive charge, against the repulsive force from the positive charge already there. Like charges repel. Therefore, electric potential lines around a positive charge are positive, as work is done per unit positive charge to bring a positive test charge from infinity to a point in the field.
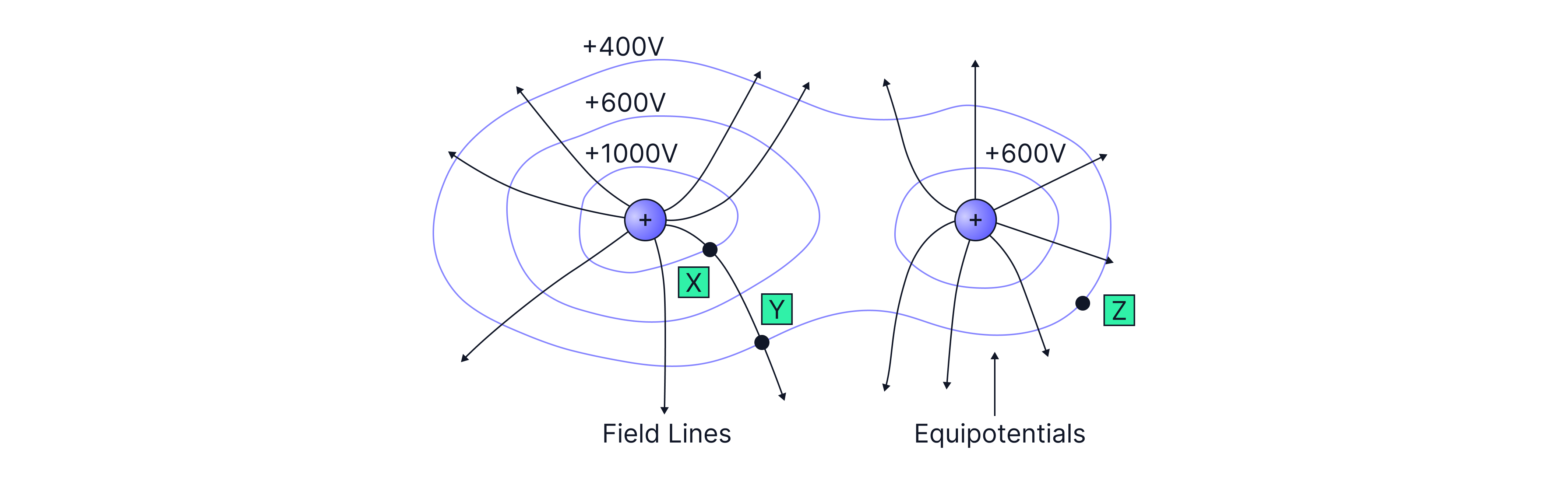
We can calculate the work done or energy required to bring the proton from infinity to point Z.
Remember: As infinity is defined as zero potential, the change in potential from infinity to = = .
Points & on the image above are on the same equipotential lines – lines of equal potential; no work is done to move between these points.
To move an electron from point to on the image above, energy is required as work is done on the electron to move it against the attractive force from the positive charge. Opposites attract.
A graph of electric potential against distance from a positive point charge is a reciprocal graph. The electric potential around a positive point charge is positive and decreases with distance, following an inverse relationship as shown by the equation:
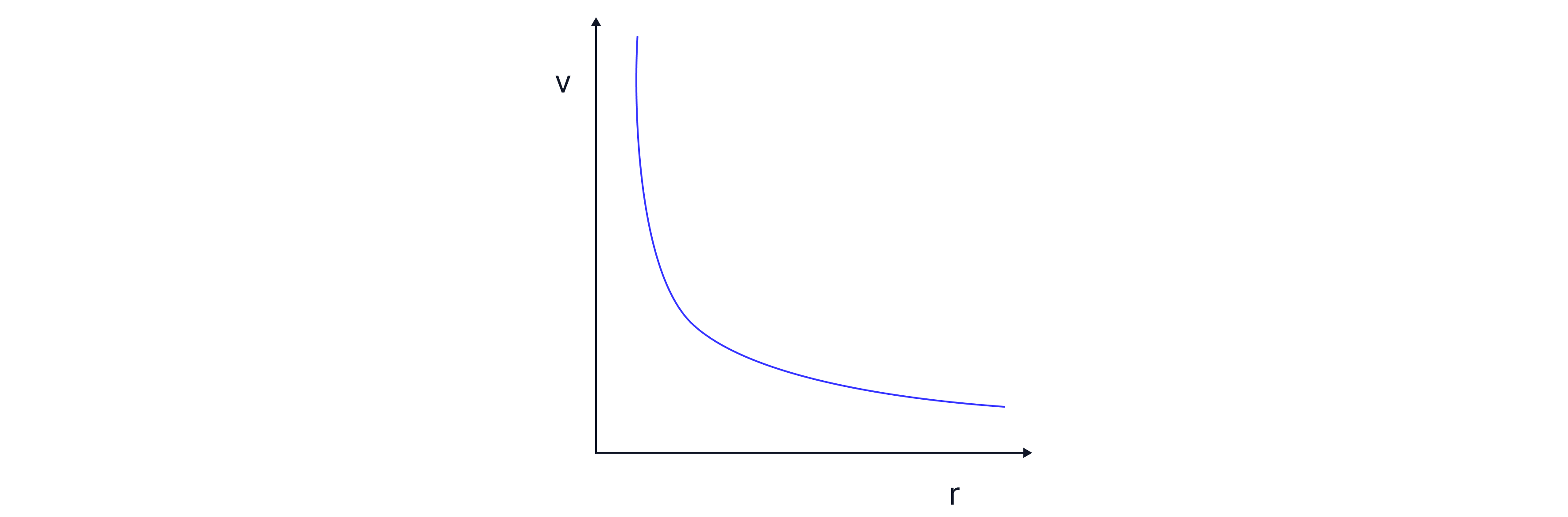
Remember: A reciprocal graph follows the equation, , not touching the axis at any point.
The gradient of the graph , gives the electric field strength, .
Worked Example
Explain why the electric potential around a negative charge is negative.
Answer:
Electric potential is the work done per unit charge to bring a positive charge from infinity to a point in a field. Since the charge is negative, it attracts the positive charge, so no work is done to bring them together – energy is released instead.
Worked Example
Calculate the electric potential, at a point from a proton.
Hence calculate the ionisation energy of an electron placed at this point, in .
Answer:
Teacher Tips: is often simplified to the constant . In question two, ionisation energy is the energy required to completely remove an electron from the field to infinity, where the electric potential is defined as zero. To convert from joules to electronvolts, you divide by the charge of an electron.
Worked Example
Calculate the potential at a distance of from a charge of .
Determine the work done to move a proton to this point in the field. Explain the sign.
Calculate the work done to move the proton to from .
Answer:
negative since energy is not required but instead released as the proton is attracted to the negative charge.
Teacher Tips: For question three, the electric potential had to be calculated at and separately, using the equation to calculate the electric potential and using as the charge.
Electric potential energy
The potential energy held by an electric charge due to its position in an electric field.
To calulate the EPE we combine the two equations:
and to get:
We can use this to calculate the closest approach of the alpha particle in the alpha scattering experiment by Rutherford, allowing us to estimate the nuclear radius (more on this in topic 11).
Worked Example
An alpha particle is fired at a gold nucleus ( protons) with of energy. The alpha particle is brought to rest at point , a distance from the centre of the nucleus.
Calculate the distance of closest approach, which tells us an approximation for the nuclear radius.
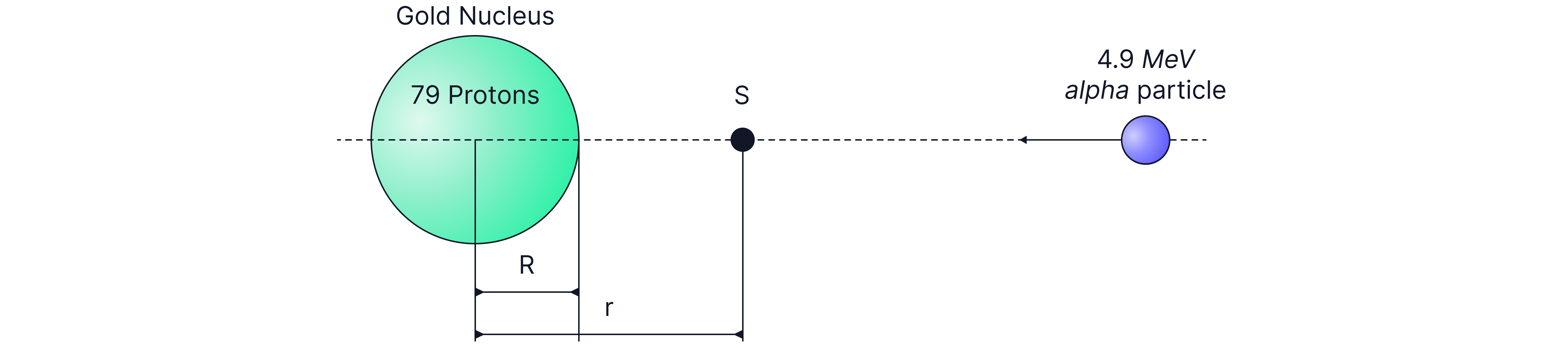
Answer:
Step 1: Convert from MeV to J.
Step 2: Assume that at closest approach, all kinetic energy is transferred to electric potential energy due to repulsion between the positively charged nuclei. All EkEPE.
Step 3: Substitute in the values (Remember: Alpha particles have a relative charge of ).
Practice Question
Two charged particles, and , are separated by a distance of . is a point on the line between and where the electric potential is zero.

Determine the distance from to ?
-> Check out Brook's video explanation for more help.
Answer: