Energy and Mass
Brook Edgar
Teacher

Explainer Video
Binding Energy
Einstein’s Theory of Special Relativity tells us that energy and mass are interchangeable.
Formula:
The strong nuclear force pulls the protons and neutrons together when a nucleus is formed, so they lose potential energy. This explains why when a nucleus is formed, energy is released due to the change in mass.
The mass of a nucleus is therefore less than the mass of the protons and neutrons that it is made of.
Let's look at Helium as an example:
Mass of Helium nucleus = .
Particle | Mass (kg) | Mass (u) |
|---|---|---|
Proton | ||
Neutron | ||
Electron |
Helium is made of two protons and two neutrons, , we can calculate the total mass of the nucleons by using their mass numbers above (also found on the AQA data sheet).
We can see that the total mass of the nucleons is more than the mass of the helium nucleus. We can calculate this change in mass and then use the equation, , to calculate the energy released on forming the nucleus.
The binding energy of a nucleus is the energy required to separate a nucleus into its individual nucleons.
The energy required to separate a nucleus into its individual nucleons is the same as the energy released when a nucleus is formed. Therefore, above we calculated the binding energy of the helium nucleus, .
The binding energy per nucleon tells us how much energy we need to put in to remove one nucleon from the nucleus.
Remember: The top number is the mass number, the total number of protons and neutrons inside the nucleus. The bottom number is the atomic number, the total number of protons inside the nucleus. So, to determine the total number of neutrons, we simply subtract the top and bottom numbers.
Worked Example
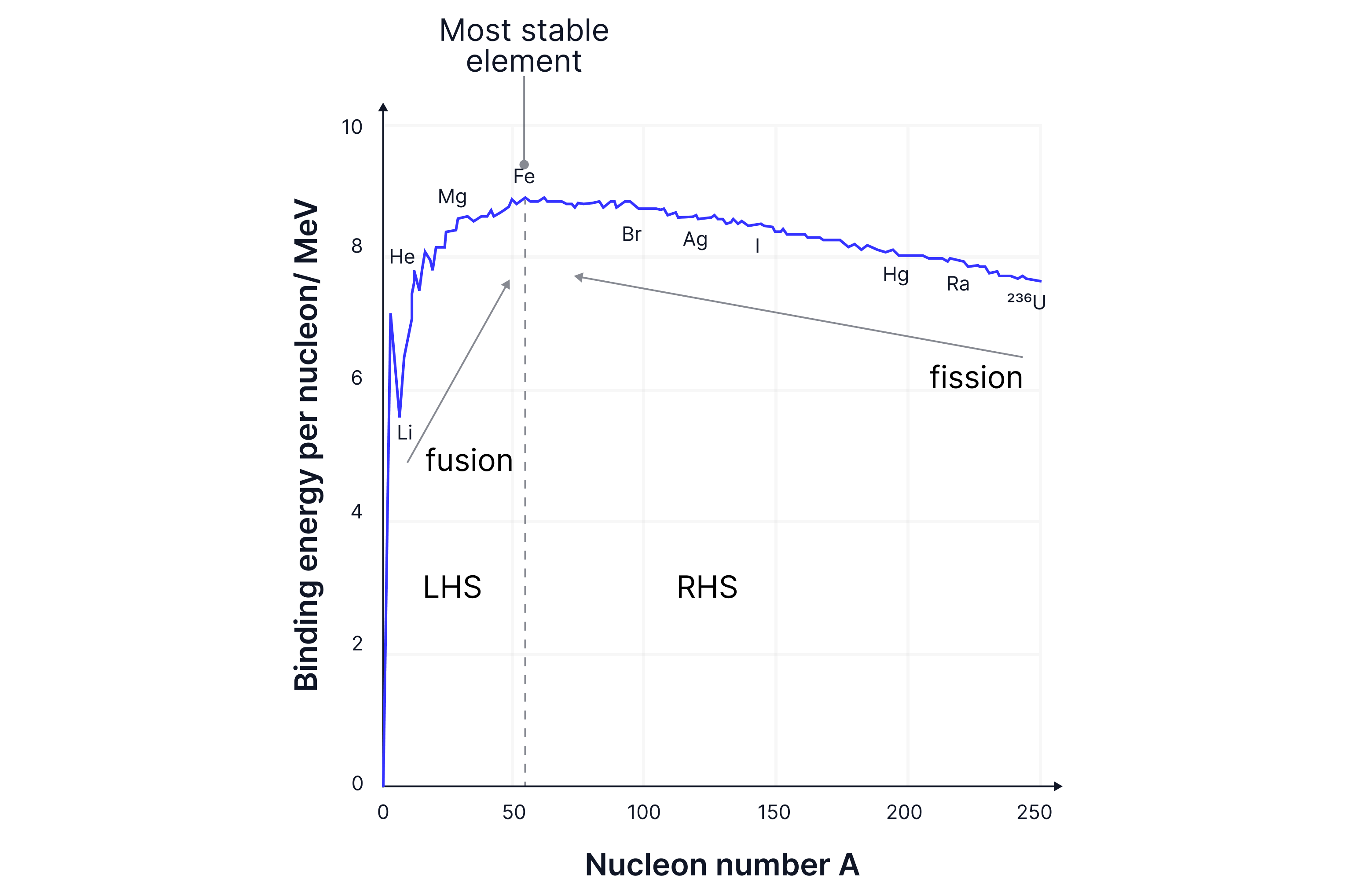
Iron-56 requires the most energy to remove a nucleon from the nucleus - iron is the most stable nucleus (it is the heaviest element that can be formed in a star).
Calculate the binding energy for a nucleus of iron (mass number , atomic number ) in
Mass of Iron-56 nucleus =
Particle | Mass (kg) | Mass (u) |
|---|---|---|
Proton | ||
Neutron | ||
Electron |
Answer:
First, we need to figure out how many protons and neutrons there are in the nucleus.
Total mass of protons and neutrons
There is an increase in energy required to remove one nucleon from the nucleus, an increase in binding energy, up until ~ -> iron. Iron-56 requires the most energy to remove a nucleon from the nucleus -> iron is the most stable nucleus.
Practice Questions
Calculate the binding energy for a Helium nucleus. (2 protons and 2 neutrons)
Mass of He nucleus =
-> Check out Brook's video explanation for more help.
Answer:
Calculate the binding energy per nucleon for a Be-7 nucleus. (4 protons)
Mass Be-7 nucleus is .
-> Check out Brook's video explanation for more help.
Answer:
Total =
Per Nucleon =
Teacher Tip: Divide the total by seven, the total number of nucleons, to find the energy per nucleon.
Uranium-236 undergoes nuclear fission to produce Barium-144, Krypton-89 and free neutrons. Calculate the energy released in this process?
Nuclide | Binding Energy per Nucleon (MeV) |
7.5 | |
8.3 | |
86 |
-> Check out Brook's video explanation for more help.
Answer: