Principle Of Superposition
Brook Edgar
Teacher

Explainer Video
Superposition
The principle of superposition states that when two waves meet, the total displacement at a point is equal to the sum of the individual displacements at that point.
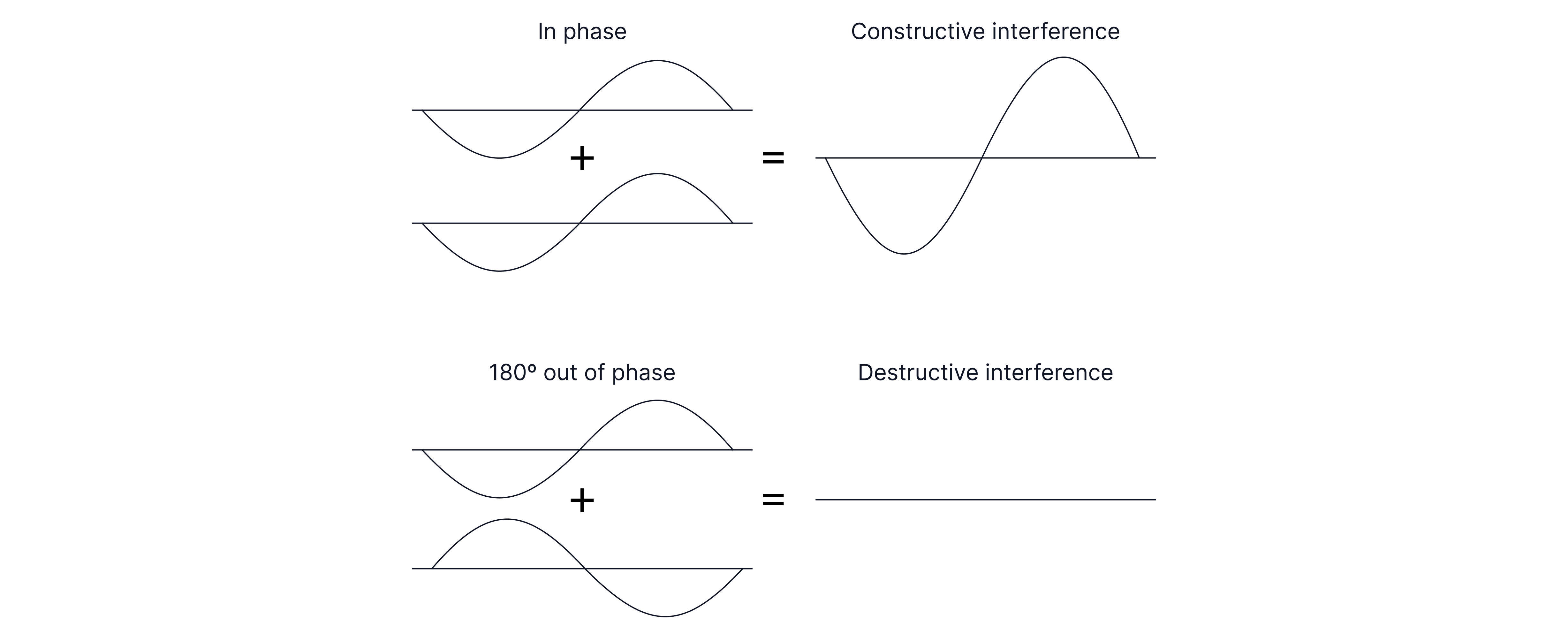
When two waves meet and superpose in phase(, even multiple of ) a maximum is formed. This is called constructive interference.
When two waves meet in antiphase (, odd multiple of ), they superpose destructively and a minimum is formed. 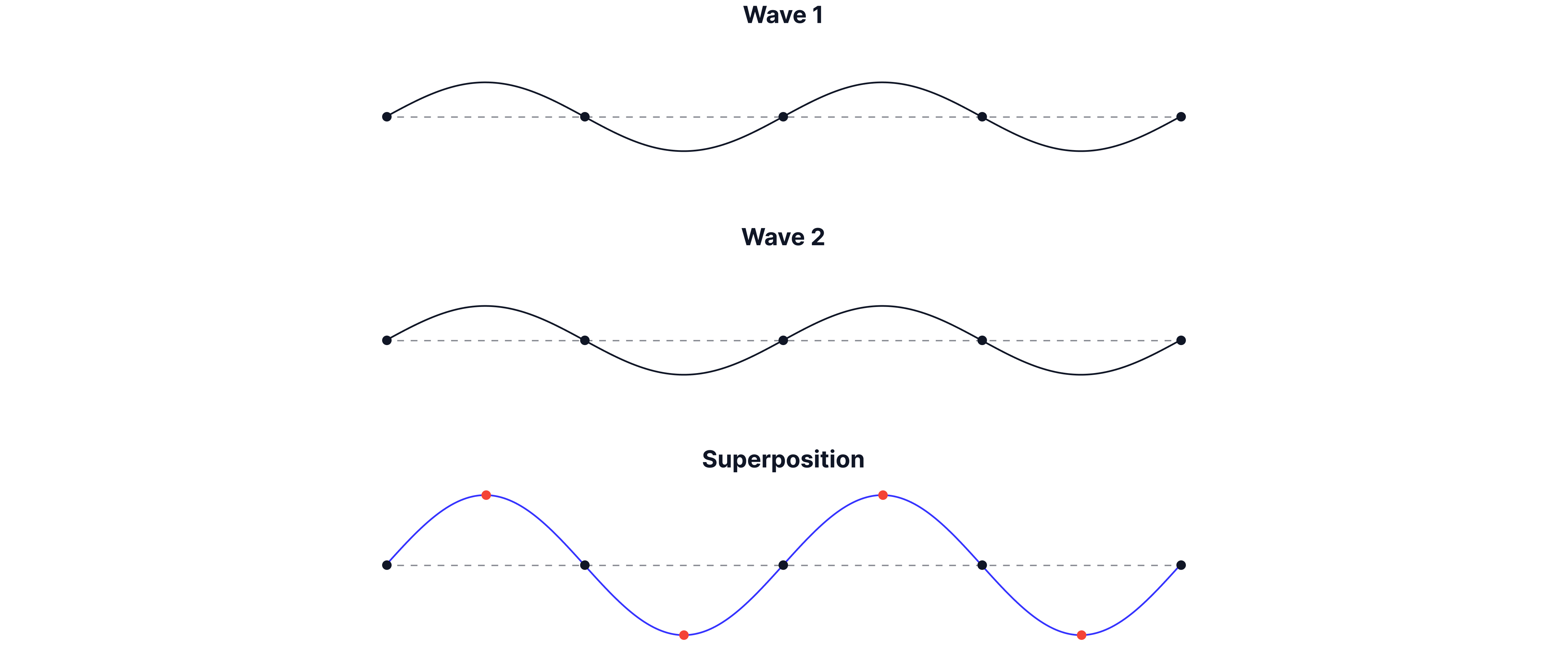
Standing waves
A standing wave, also known as a stationary wave, does not transfer energy. They are formed from the superposition of two waves of the same frequency and amplitude travelling in opposite directions.
-> This is usually achieved by having a travelling wave (progressive wave) reflecting on itself.
Standing waves are formed of nodes and antinodes.
Node: a point of zero displacement as a result of destructive interference, occurs when two waves meet in such a way to give zero displacement, such as when a point of maximum displacement on one wave meets a point of minimum displacement on another or when two points with zero displacement meet.
Antinode: a point of maximum displacement due to constructive interference, when a maximum displacement on one point of a wave meets a maximum on another.
All points between two nodes on a standing wave are in phase (they oscillate with the same frequency, and all points reach maximum and minimum displacement at the same time). This is also true if the points are separated by an even number of nodes.
Points that are separated by a node are exactly out of phase, i.e. antiphase (reach their maximum and minimum displacement at opposite times). This is also true if the points are separated by and odd number of nodes.
To summarise:
Worked Example
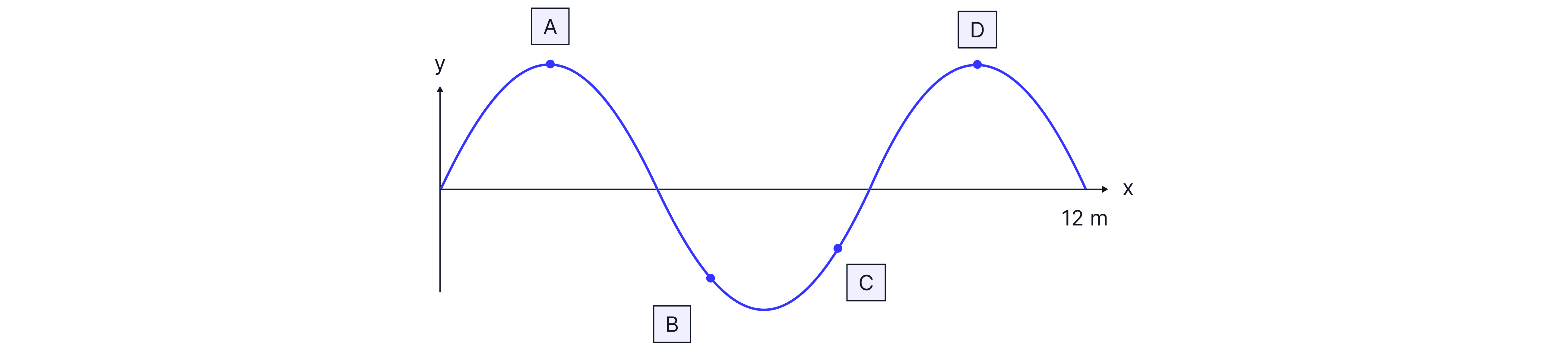
The image shows a standing wave. State the phase difference of the points below on this wave,
A and B
A and C
A and D
B and C
Answer:
A and B: exactly out of phase,
A and C: exactly out of phase,
A and D: In phase,
B and C: In phase,
Teacher Tip: Points B and C are in phase because this is a standing wave. Points on a standing wave are in phase if they are between the same nodes because they will move in the same direction at the same time.
Worked Example
The diagrams below show snapshots of a wave taken every millisecond.
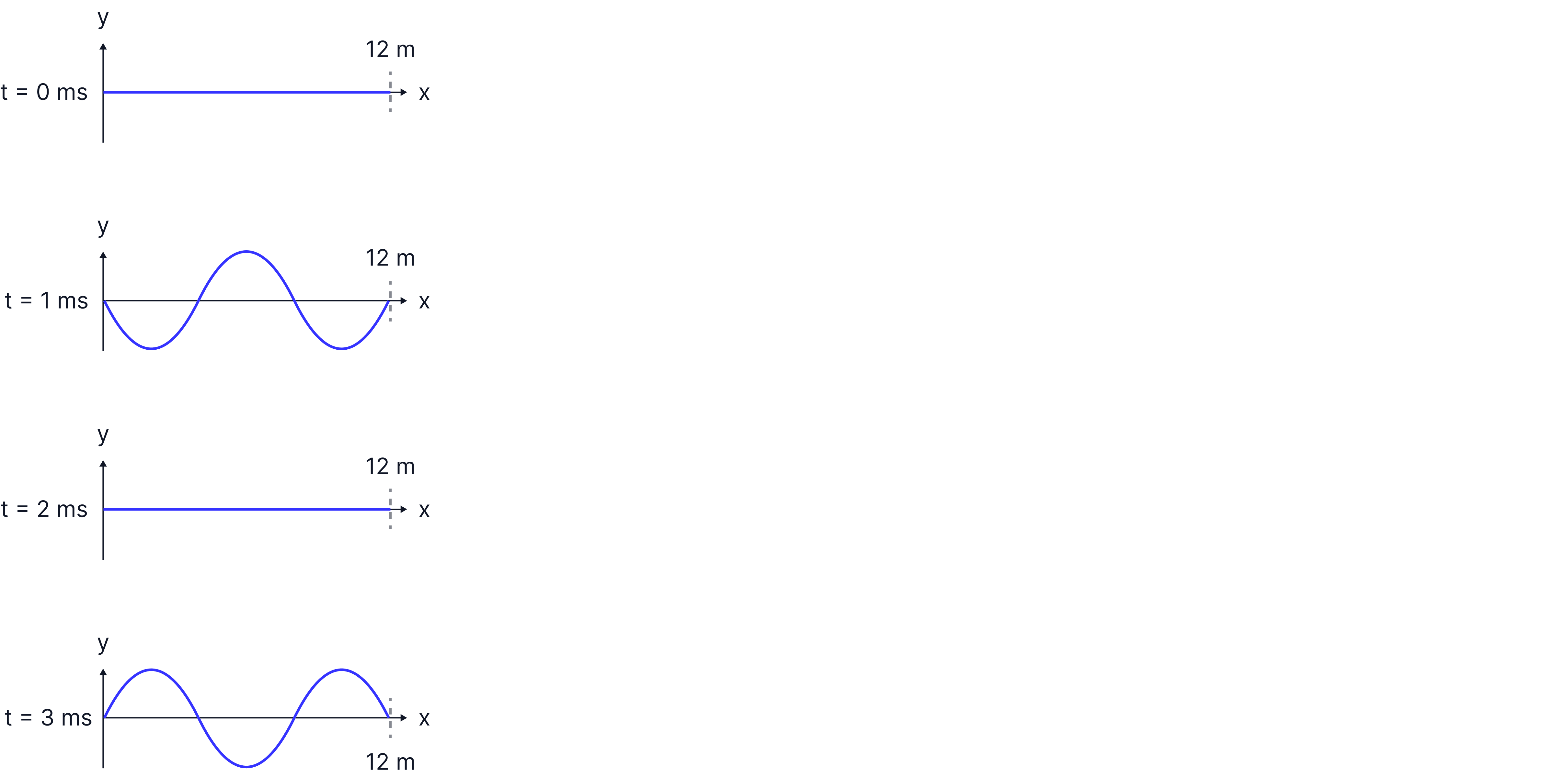
Explain how the diagram shows this is a stationary wave.
Determine the wavelength of the wave.
Determine the frequency of the wave.
Sketch the stationary wave at .
Answer:
Nodes can be seen -> points that always have zero amplitude, whereas on a progressive wave, all points have the same amplitude.
Looking at the third harmonic, the second image, we can see that the length of the string covers waves.
It takes two milliseconds to move from zero displacement to one extreme and back again, so a full cycle will take four milliseconds.
Same as at and , flat along the equilibrium line.

Harmonics
Stationary waves formed on strings, fixed at each end, can only occur at certain frequencies. These are called harmonics and have different wave patterns.
To form the first harmonic, also known as the fundamental mode, a string is fixed at each end and made to vibrate. The frequency of vibration is gradually increased until the first harmonic is seen. The first harmonic is a single loop, where the length of the string is equal to half of the wavelength , .
->
Harmonics are used in musical instruments like guitars.

Worked Example
The speed of waves, , is fixed. Give the expression for the frequency of the second harmonic.
Answer:
The second harmonic has two loops and the length of the string is equal to the wavelength.
If the speed of the wave is unknown, the frequency for the first harmonic can also be found using the equation below, where wave speed, .
Formula:
Worked Example
A guitar string, mass , length is fixed at either end. The string is tightened to a tension of between two bridges, as shown below, separated by .
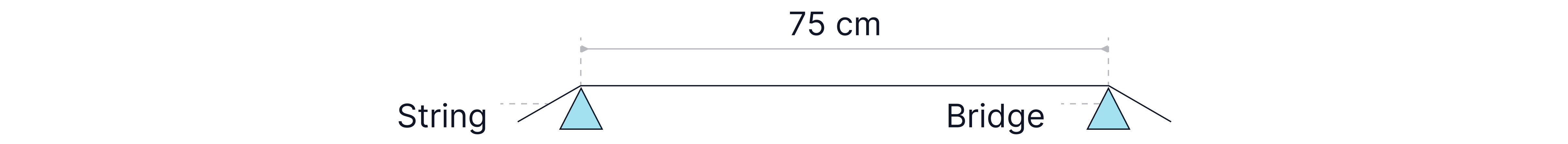
Calculate the frequency of the first harmonic produced when the string is plucked.
Explain what would happen to the speed of the wave if the tension were doubled.
Answer:
If we double the tension, , then the new speed will be a factor of root two greater than the old speed.
Practice Question
A stationary wave forms on a string.
Which is true.
The amplitude is a maximum at the nodes.
The distance between two adjacent nodes is .
Vibrations at two adjacent antinodes are in antiphase.
The time period of oscillating sections varies along the string.
-> Check out Brook's video explanation for more help.
Answer:
C)