Radioactive Decay
Brook Edgar
Teacher

Explainer Video
Radiation has many uses, such as in:
Medical imaging -> X-rays are used to produce images of bones to diagnose fractures.
Cancer treatment (Radiotherapy) -> Gamma rays or high-energy X-rays are used to kill cancerous cells in targeted areas of the body.
Radioactive tracers -> The tracer emits gamma radiation, which is highly penetrating and only weakly ionising. It concentrates in certain organs, allowing doctors to see how those organs function. The emitted gamma rays are detected outside the body using gamma cameras or PET scanners.
Sterilisation of medical equipment -> Gamma rays are used to sterilise surgical instruments by killing bacteria and viruses.
Industrial radiography -> Gamma rays and X-rays are used to inspect metal welds and structures for internal cracks without damaging the object.
Smoke Detectors -> Alpha particles from the decay of Americium- are used to detect smoke particles. When smoke enters the detector, it absorbs alpha radiation, reducing ionisation and triggering the alarm.
Carbon Dating -> Radioactive isotopes, such as carbon-, are used to determine the age of archaeological and geological samples by measuring the amount of carbon-14 remaining in once-living material.
The type of radiation used depends on its half-life, for example, you wouldn’t want to use a source of radiation with a short half-life in a smoke alarm, as they would then have to be replaced often.
Remember: We need to know how to protect ourselves from radiation by:
Minimising time spent near radioactive sources to reduce total exposure.
Increasing distance from the source and use shielding. The intensity of radiation decreases with distance following the inverse square law, .
Wear protective clothing such as lead-lined aprons, gloves, and radiation badges (film badges) to monitor radiation dose.
Using remote handling -> Using robotic arms or tongs to handle highly radioactive materials, reducing direct exposure.
Half-Life
The half-life, , of a radioactive isotope is the time taken for the number of nuclei to decrease to half the initial number.
If the half-life is very long, then the substance will remain radioactive for a very long time.
Formula:
The decay constant is found by calculating the change in the number of nuclei, , over time.
The activity, , of a radioactive sample, is the number of nuclei that decay per unit time. The activity is directly proportional to the number of nuclei. the equation can be written as, .
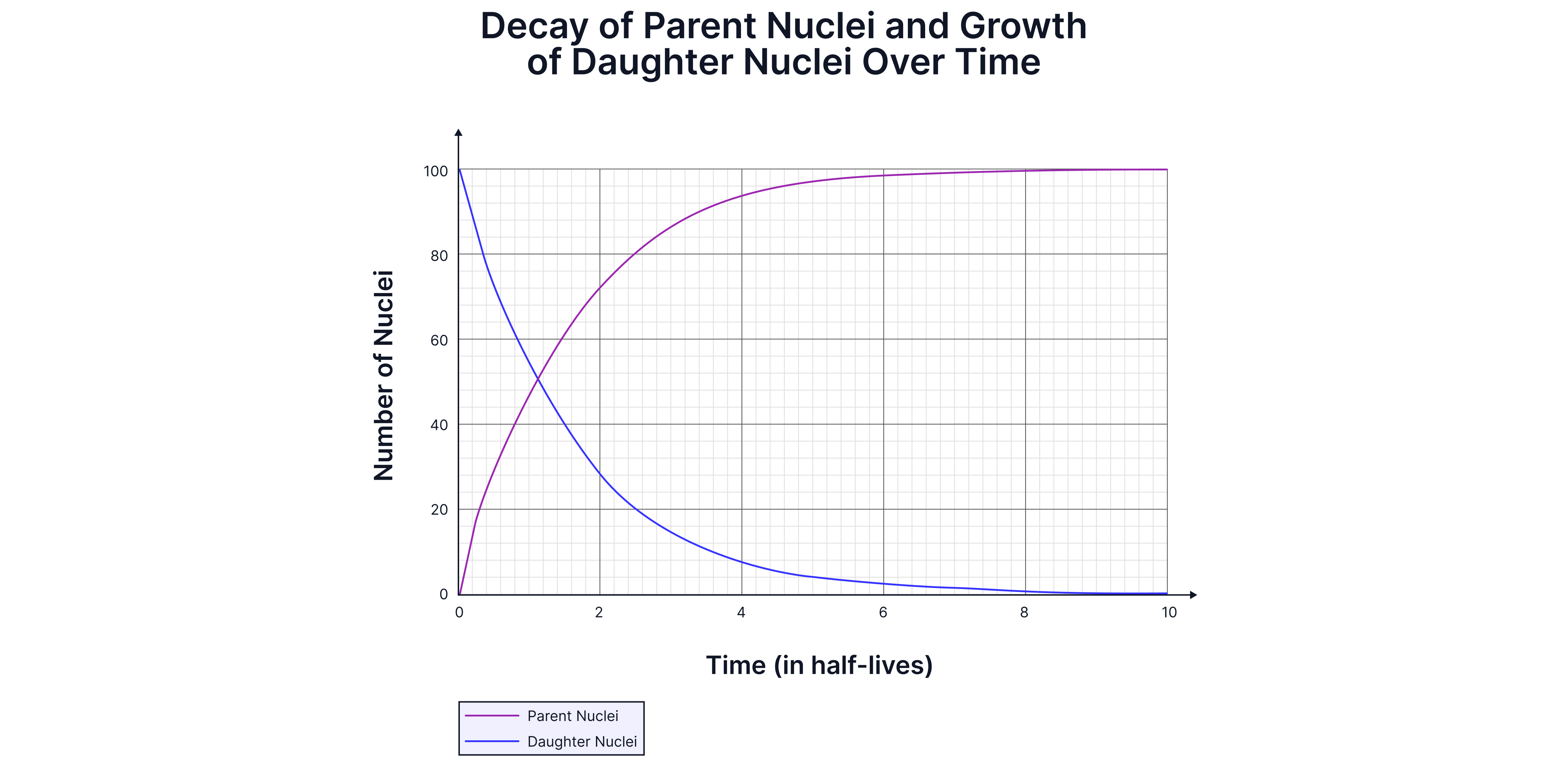
Although the number of nuclei/activity never falls to zero, in practice, it eventually falls to a level indistinguishable from background radiation.
The number of unstable nuclei decreases exponentially -> the number of nuclei drops by a constant factor in equal intervals of time. Radioactive decay can be described as exponential decay.
Formula:
As activity is directly proportional to the number of nuclei, activity can be written as, .
Sometimes, examiners, instead of giving the number of atoms , , they provide the mass. Here we need to remember our GCSE chemistry equations first reviewed in topic .
For example, if we are given of radium-, the number of nuclei present can be found by first calculating the number of moles, .
The number of nuclei is then found by multiplying this by Avogadro's constant,
We can now calculate the initial activity of radium-, with decay constant, .
The activity after days can be calculated as follows,
Remember: Activity, , and count rate, , are not quite the same thing. Activity is the number of nuclei that decay per second, whilst count rate is the number of decays detected per second, . The count rate includes background radiation, so if you want to find the corrected count rate (i.e. the count rate for the source alone), you need to subtract the background count rate.
Worked Example
Calculate the half-life of an isotope with a decay constant of .
Answer:
Worked Example
A radiographer has calculated that a patient is to be injected with atoms of iodine- to monitor thyroid activity. Half-life days. Calculate:
The radioactive decay constant.
The initial activity.
The number of undecayed atoms of iodine- after days
The total activity after days
Answer:
N-Z Graphs
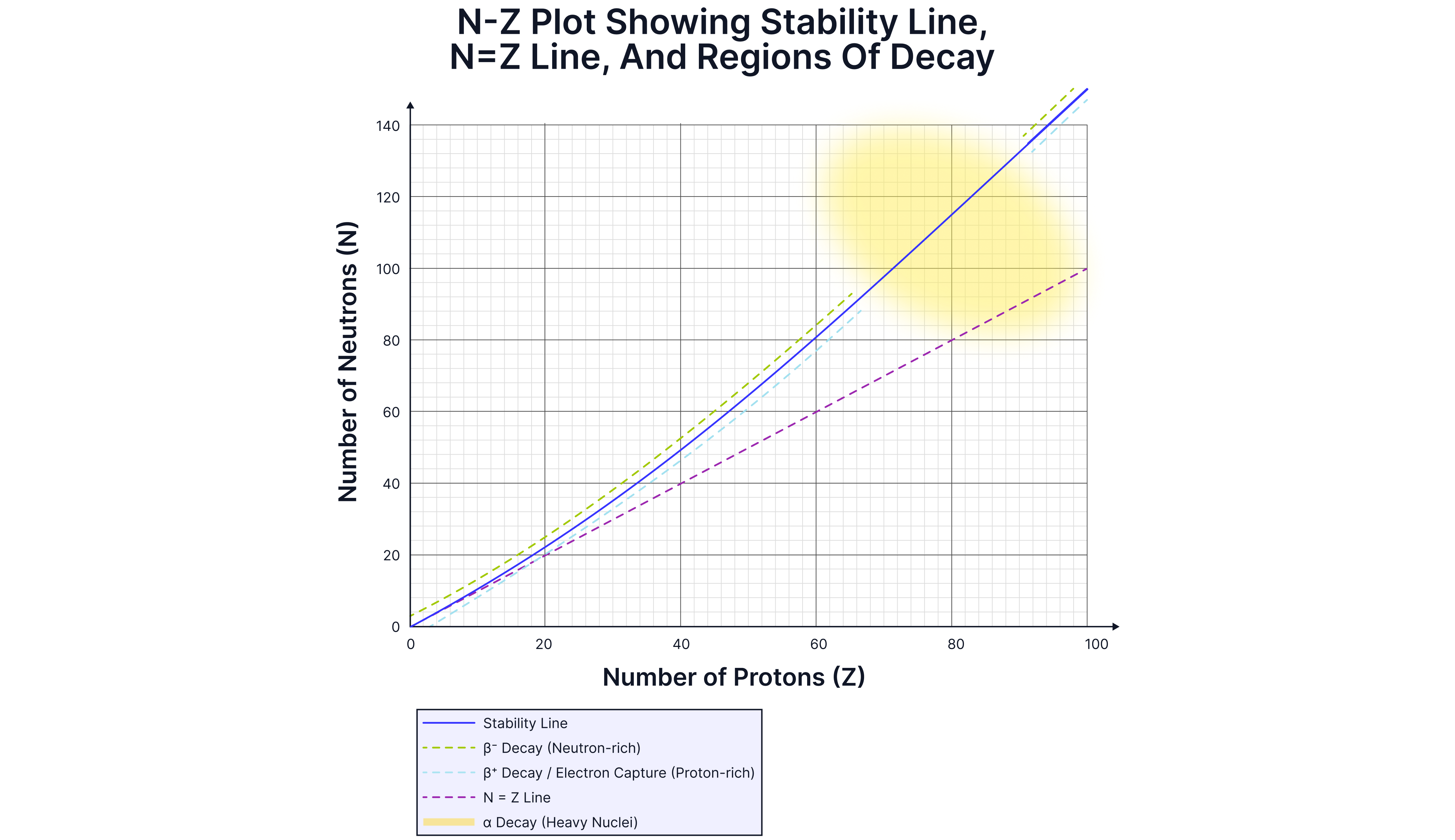
For light elements (Z < ), we can see that the stability line follows the, line. That the number of neutrons, , is roughly equal to the number of protons, . However, as the elements get heavier, stable nuclei require more neutrons than protons. The extra neutrons help bind the nucleus together; more protons would increase the electrostatic repulsive force (trying to pull the nucleus apart). More neutrons are needed for the strong force to overcome the Coulomb repulsion the line of stability bends upwards.
Different types of decay occur in different regions on the graph:
emitters (). The nuclei have more neutrons than protons but are too large to be stable, as the strong nuclear force between the nucleons is unable to overcome the electrostatic repulsion between the protons.
emitters (above the stability line/to the left of the stability line). Neutron-rich, they become more stable when a neutron decays into a proton.
emitters (below the stability line/to the right of the stability line). Proton-rich, they become more stable by a proton decaying into a neutron.
Worked Example
Which type of nuclei undergo beta negative decay?
Write an equation to represent this.
Answer:
Nuclei which have too many neutrons.
Beta minus decay emits a beta negative particle (a fast-moving electron).
Worked Example
State which type of radiation is used in radioactive tracers and why.
State two reasons why gamma radiation may be emitted from the nucleus after decay.
Answer:
Gamma radiation, as it is the most penetrating type of radiation so can easily exit the body and thus be easily detected. We use a source with a short half-life, so it doesn't stay inside the body for long. It is also the least ionising type of radiation. Technetium- is one of the most common tracers; it is a pure gamma emitter and can be easily prepared in the lab
During electron capture. A proton absorbs an inner shell electron, causing an upper shell electron to fall down to replace the inner shell electron. A gamma ray is emitted. Also, following another type of emission, a nucleus may be excited and then deexcite, emitting a gamma ray.
Worked Example:
Strontium- is a beta emitter. It is one of the radio-nuclides found in the fallout from an atomic bomb explosion. It can be absorbed into the bone. It emits beta particles and has a half-life of years. Calculate the time needed for the activity to fall to % of the original.
Answer:
To calculate the time taken, we first need to calculate the decay constant.
We need to take natural logs of each side and use our log rules.
Teacher tip: Because the decay constant was left in years, your answer should also be in years.
Energy Level Diagrams
Energy level diagrams show us possible decay routes.
For example, magnesium decays by beta minus decay into two possible excited states of aluminium. Both excited states decay by emission of a gamma photon directly to the ground state; one route produces a gamma photon with a higher frequency than the other.
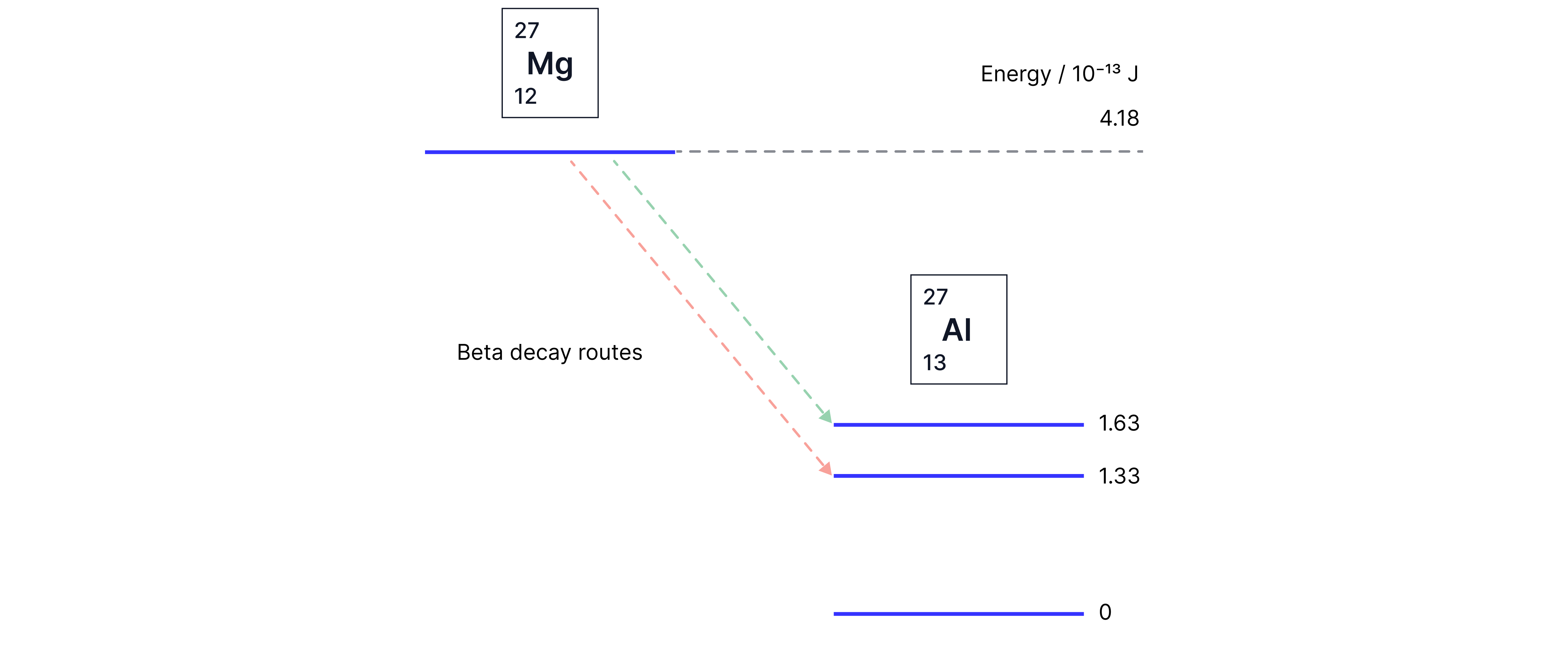
Green path: Mg can decay into Al by emitting a beta particle. It decays into Al at the energy level. The nucleus is excited, so it decays to by emitting a high energy gamma ray.
Red path: Mg can decay into Al at the energy level by emitting a beta particle. The Al nucleus is excited, so it emits a gamma ray to get to .
We can calculate the minimum possible kinetic energy of the emitted beta particle. The beta particle will have the least energy when the emitted gamma ray has the most energy. This is the green path.
Diagrams can also be used to show multiple decay paths, like the example below:
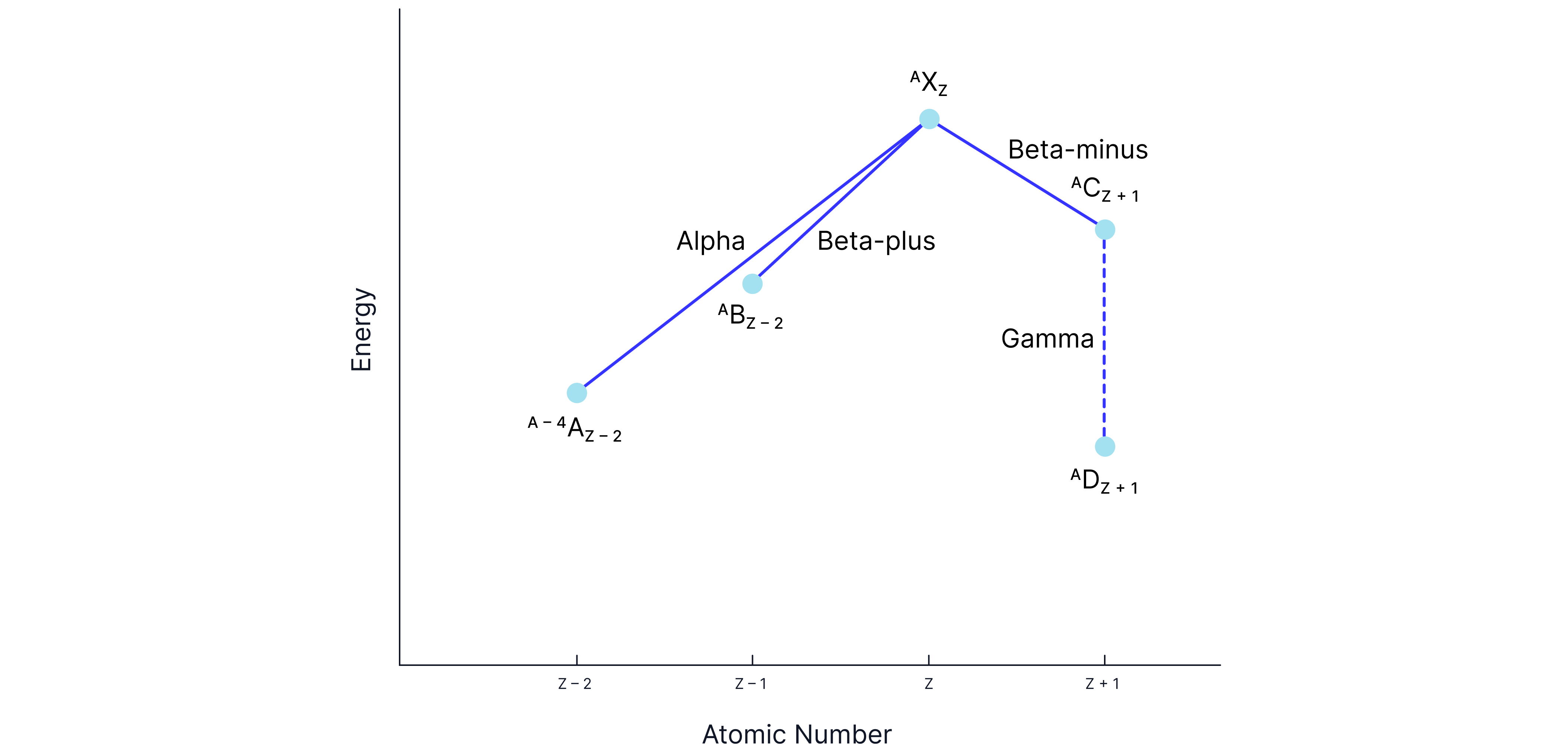
Alpha decay, emitted:
The nucleus loses two neutrons and two protons
The point shifts to the left two and down in energy
Beta minus decay:
Occurs when a nucleus has too many neutrons,
The point shifts to the left one and down in energy
Beta plus decay:
Occurs when a nucleus has too many protons,
The point shifts to the right one and down in energy
Gamma decay:
No change in atomic number
The point shifts down in energy
Remember: The atomic number = the number of protons.
Worked Example
A nucleus of polonium, Po, may decay to the isotope of lead Pb-. On the graph below, draw four arrows to show the sequence of changes to and that occur as the polonium nucleus changes into the lead, Pb- nucleus.
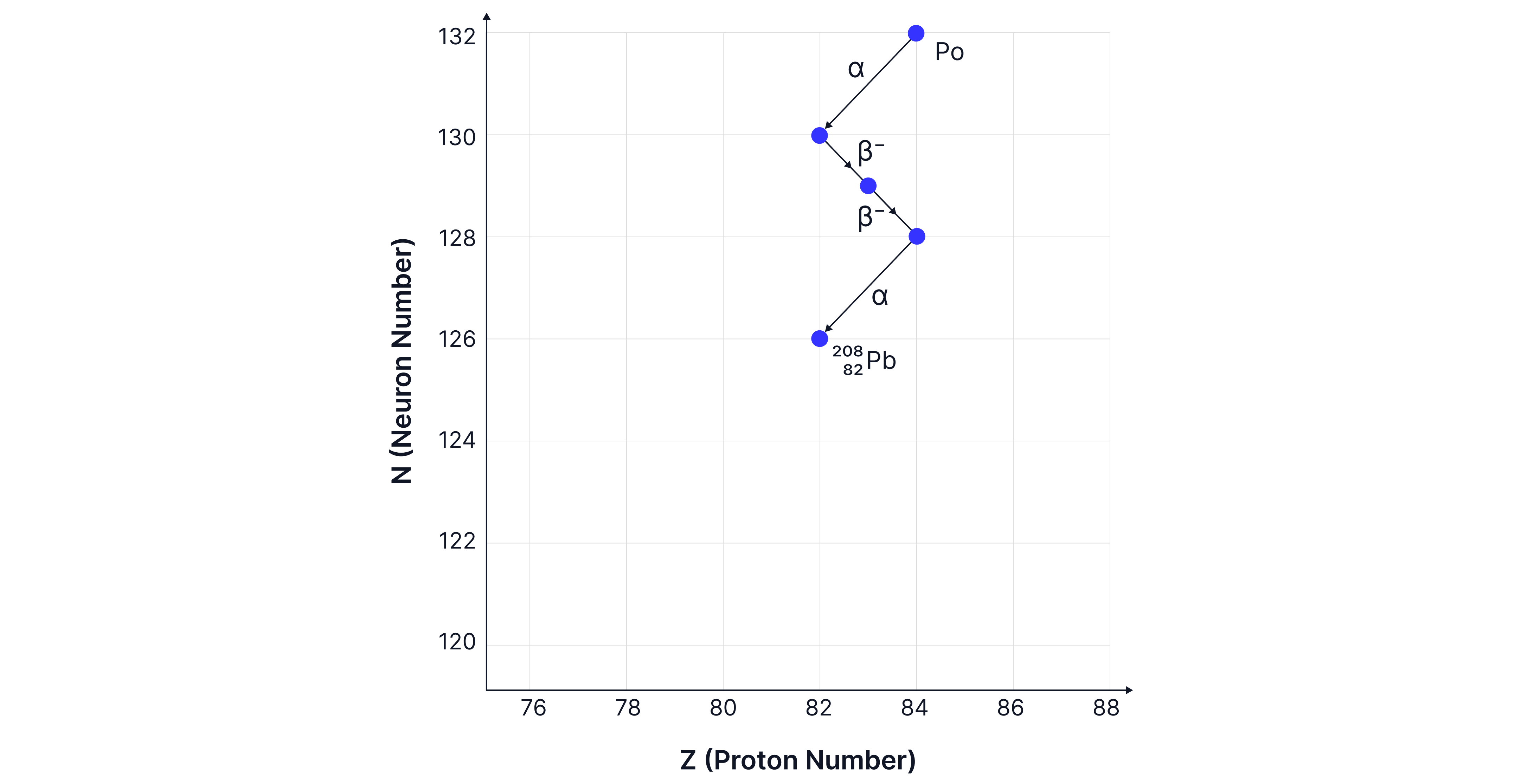
Two alpha and two beta minus decays occur.
Practice Questions
Cobalt- has a half-life of years.
Calculate the activity of
-> Check out Brook's video explanation for more help.
Answer:
State the decay equations for Beta minus and Beta positive decay.
-> Check out Brook's video explanation for more help.
Answer:
Minus:
Positive: